Lalitha Sundaresan
Increasingly it is felt that spatial sense is necessary to understand and appreciate mathematics. Several studies have shown that young children exposed to the idea of shapes and how shapes change when rotated, enlarged, etc., are more comfortable with mathematics as they grow older.
In India, formal introduction of geometric shapes and the inter-relationships of shapes is introduced in grade 1. Children are introduced to shapes like triangles, squares, rectangles at this stage. Measurements of size is introduced later on. The idea of big and small are however intuitively taught.
Properties of these shapes like perimeter and area are introduced by grade 3 or 4. Since children are still not familiar with units of measurement and dimensions, these concepts are difficult to introduce and also understand.
Tangram tiles or pieces are very useful in this regard. This article aims to illustrate how tangram tiles can serve the purpose of both fun in the class as well as some learning of these two concepts – perimeter and area.
What is a tangram?
A tangram is a Chinese puzzle consisting of seven flat tiles. The tiles include five triangles, one parallelogram and one square. The original puzzle requires that all seven tiles be used to form a variety of shapes. Although many children are encouraged to work on tangram puzzles to improve their spatial skills, tangram tiles have other uses too.

Making your own tangram tiles is quite simple and requires only a thick square chart paper or cardboard. The following diagram will illustrate how to get the seven pieces.
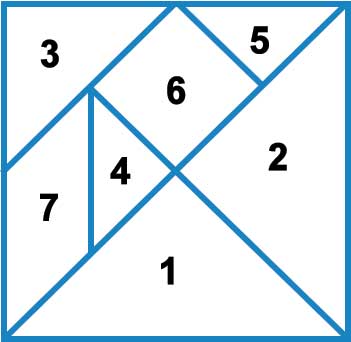
Start with a square of suitable size and draw the lines indicated in the figure and cut out the pieces. Teachers will note that the sides of the tiles are not rational numbers. The seven pieces will have the following sides if the original square was of length 1 unit.
| Tile | Shape | Side / base | Side / Height | Hypotenuse |
|---|---|---|---|---|
| 1 | Right Triangle | √2/2 | √2/2 | 1 |
| 2 | Right Triangle | √2/2 | √2/2 | 1 |
| 3 | Right Triangle | 1/2 | 1/2 | 1/√2 |
| 4 | Right Triangle | √2/4 | √2/4 | 1/2 |
| 5 | Right Triangle | √2/4 | √2/4 | 1/2 |
| 6 | Square | √2/4 | ||
| 7 | Parallelogram | 1/2 | √2/4 | 1/4 |
For the purpose of this article we will follow the labels provided for the tiles.
The perimeter and area of these tiles are also shown in the table below:
| Tiles | Perimeter | Area |
|---|---|---|
| 1, 2 | 2.14 | 0.25 |
| 3 | 1.57 | 0.125 |
| 4,5 | 1.07 | 0.625 |
| 6 | 1.14 | 0.125 |
| 7 | 1.57 | 0.125 |
Develop spatial skills
Early on, children do become familiar with shapes such as triangles, squares, and rectangles. The tangram tiles can be used to emphasize this to start with. It is not necessary to use all the seven tiles to create shapes.
- The teacher can ask children to identify shapes, pick up identical ones in terms of shape, size; ask them to place one tile on top of another to find out if they are identical.
- Demonstrate how two triangles combine to form a square.
- There is no rectangular tile here. Ask children to form a rectangle with the given tiles. Children are bound to come up with several ways to do this.
- Parallelogram is a new shape for them. Ask them to form parallelograms with the given tiles.
Measurements and perimeter
Children can be taught to measure the sides of these tiles using a thread to demonstrate that
i) The sides of the triangles are not all equal.
ii) Two sides of the triangle are equal.
iii) What isosceles triangles are.
iv) Difference between rectangles and squares.
The following two rectangles can be formed by the children.

First ask the children to use a thread to measure the length and breadth of the two rectangles. Are the two rectangles identical? If we remove tiles 1 and 2 do we still have a rectangle?
Now to the perimeter. Take tile 6 which is a square. Starting from one vertex of the square, using a thread, ask the children to go north, then east, south and west to come back to the starting point. Introduce the idea of perimeter at this stage.
The teacher could ask the children to find the perimeters of all the seven tiles. Children may find some surprising results here.
This way of measuring helps to introduce the idea of directions also (north, east, west and south). They could also experiment starting at the south-eastern corner and move the thread north, west, south and east and find that the perimeter or distance travelled is the same irrespective of the route taken!
By grade 4 children are taught to use a foot ruler and they can be encouraged to write down the actual perimeter in centimetres.
At this stage they will also discover that different shapes can have the same perimeter. For example tiles 3 and 7 have the same perimeter, but different shapes.
Area
Area is a more difficult concept to introduce. The teacher can introduce area as the space contained within the perimeter of an object. Larger the space inside, larger the area.
Take for example, a kitchen towel, a bath towel and a rectangular doormat. Spread them on the floor. It is immediately apparent to the children that the bath towel occupies more space than the door mat and the kitchen towel.
Tiles 1, 2, 3, 4, and 5 are all triangles. The children can be asked to order them in terms of area. Larger to smaller. By placing tile 1 on top of tile 2 they can be taught that they both have the same area. Similarly tiles 4 and 5.
What about tiles 3, 6 and 7?
Place tiles 4 and 5 on top of tile 6 to show that the area of tile 6 is the sum of the areas of tiles 4 and 5.
Recall that we have not introduced the notions of measurement units or dimensions.
Now ask the children to find the area of tiles 3 and 7, the parallelogram using the other tiles.
Tangram puzzles
At this stage, introduce the children to the tangram puzzle. The children should use all the seven tiles to create shapes such as the ones given below.

Once these shapes are created using all the seven tiles, tell them that all the three shapes have the same area, because the area is the sum total of the areas of the seven tiles.
Ask the children to find the perimeter of these shapes. Are they all the same? Which one has the largest perimeter?

Introduce the idea that although the area of an irregular shape such as the one given below can be determined by summing up the areas of the regular shapes that constitute it, the same cannot be said for its perimeter.
Another simple exercise will be to find the perimeter and area of the following three shapes using all the seven tiles.

More activities
Children can now be introduced to the idea of how rectangles can be constructed with the same area but different perimeters. Cut out or draw rectangles of size 6 X 6, 9 X 4, and 12 X 3. All of them have the area 36 in appropriate units. Their perimeters are respectively 24, 26 and 30 units.
Let us take another example of two rectangles of sizes 16 X 2 and 9 X 4. Their areas are 32 and 36 respectively. So, children will recognize that rectangle 2 is larger than rectangle 1 in terms of area. Their perimeters however, tell a different story. Rectangle 1 has a perimeter of 36 and rectangle 2 has a perimeter of 26. So if you have to go around these two rectangles, you will cover a larger distance in the case of rectangle 1.
Conclusion
Tangram puzzles help children develop and improve spatial skills. Using the seven tiles of the tangram, children can be given an intuitive idea of perimeter and area of regular and irregular geometric shapes.
These puzzles help to reinforce the point that perimeter and area are not related in any way.
Tangram puzzles can be used to illustrate that irregular shapes having the same area can have different perimeters. In other words shapes having identical areas need not have identical perimeters.
The author is with the National Institute of Advanced Studies, Bengaluru. She has a Ph.D from the Indian Statistical Institute. She is interested in satellite image analysis and occasionally dabbles with school mathematics. She can be reached at sundaresan.lalitha@gmail.com.
