Shikha Takker
I was observing an introductory lesson on decimals in grade 5. The teacher began by recalling the place value of the digits in the number 739. Students repeated the place value of each digit after her, “Seven hundreds, three tens and nine ones”. The teacher then changed the number to 7.39, drawing students’ attention to the dot and defining it as the decimal point. She added that the digits before the decimal point are a whole number. She mentioned that the place value names of the digits to the right side of the decimal point are like the whole number names, “Like tens on the left side, there is tenths on the right side, (emphasizing-ths in tenths).” She introduced tenths, hundredths and thousandths by establishing the correspondence between the place value names on either side of the decimal point. A student almost immediately asked, “Teacher, where is oneths?” There was a pause for a moment in the class after which the teacher answered, “There is no oneths.” She then moved on to place the decimal number in the place value table.
In another introductory lesson on decimals, the teacher recalled length measures. Students followed her explanation of the length of a pencil as 3 centimetres 5 millimetres. The teacher gave a few more examples: 5cm 2mm, 1cm 4mm, 6cm 9mm, etc. She then told the students that 3cm 5mm can be written as 3.5 cm, where the point separates the centimetres from the millimetres. The students were expected to follow the pattern and extend this representation to the other lengths: 5.2 cm, 1.4 cm, 6.9 cm. A student then asked, “Teacher why centimetre?*” to which another student added, “Haan, why not millimetre?” The teacher moved on to explaining the place value names of the digits on the left and right side of the decimal point. She mentioned how in 56.78 cm, the place value of 5 is tens. Similarly, she added, the place value of 7 is tenths. Another student asked, “Teacher, seven should be oneths na?” The teacher answered, “The place value of 7 is tenths and not oneths.”
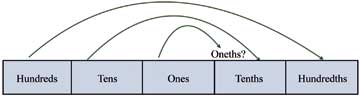
The “oneths” question raised by the students is intriguing. It seems reasonable that if there is a correspondence between the names of the whole number part (tens, hundreds, thousands) and the fractional part (tenths, hundredths, thousandths) of a number, then the same has to be true for the ones place value. The explanation of extending the names from the left side of the decimal point to the right side does not hold for a corresponding position for ones, why?
Before we understand the reason for the missing oneths, it is important to acknowledge that the question arose from the students in both the lessons. Selecting such mathematically potent ideas from a variety of students’ utterances is one of the tasks entailed in the complex work of teaching. I refer to those student ideas as ‘mathematically potent’ which have the potential to unpack some key mathematical ideas. Such ideas can be used by a teacher as a learning opportunity for the whole class. What kind of knowledge do teachers need to deal with such ideas in the classroom?
Knowing content and students
We all agree that a teacher needs to know the content to be taught. One of the sources of this content is the textbook. However, handling students’ questions arising during the course of teaching requires knowledge that is beyond the content knowledge represented in the textbooks. Additionally, handling unexpected student questions requires the knowledge of the content and the skill of dealing with it in the whole class. In the literature on mathematics teacher knowledge, such a combination of skill and knowledge is called knowticing (Even, 2008). Knowticing the mathematical potential of a student’s idea and handling it requires an in-depth knowledge of the content. An in-depth knowledge includes knowing why an algorithm works, what kind of representations are useful in teaching a particular topic (Ball, Hill & Bass, 2005), the prior knowledge needed to learn a topic, how it connects with the topics to be taught later, and so on. A deeper knowledge of the content supports teachers’ knowticing and vice versa.
Why is there no oneths?
Let us see why students are led to ask the question about the existence of oneths. Often, the place value names of the fractional part of the decimal number are introduced using the whole number names. The correspondence between the names of the place values is drawn around the decimal point, for instance, in references such as “left and right side of the point”. Such an explanation creates a mental mirror or symmetry between the place value names on either side of the decimal point (refer Figure 1). The mirror metaphor (MacDonald, 2008) or the symmetric relation helps the students in recalling the names of the fractional parts, that is using tens to recall tenths. Teachers use the symmetric relation to bridge students’ prior knowledge of the place value names learnt during whole numbers with the new knowledge of naming the fractional part of the decimal number. On the other hand, such an explanation requires locating the corresponding place value name for ones, that is, oneths.
The place value to the immediate left of the ones is 10 times ones and that to the immediate right is 1/10th of ones. This means that the symmetry of place value names is on either sides of the ones place value and not the decimal point. In other words, the place value of the digits to the left and right side of the ones are positive and negative powers of 10, respectively. Since, the symmetry is around the ones place value, the correspondence between place value names on either side of the ones can be drawn.
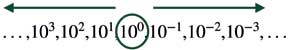
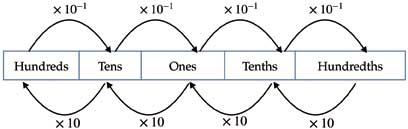
While the mirror metaphor is one way of explaining the decimal place values, there is another explanation. In a base 10 system, each consecutive place value is related to the other by a power of 10. A continuous relation between place values of digits in a decimal number (refer Figure 2) helps in understanding why oneths cannot exist.
(adapted from MacDonald, 2008)
Both these explanations for the non-existence of oneths were discussed with the teachers who taught the two lessons reported at the beginning. As the teachers discovered the reasons underlying the students’ questions, they began to look at the oneths question differently.
In the following year, the teacher began teaching decimal place value names using the continuous relation between the place values of digits in the base 10 system. A student observed the correspondence between the place value names and asked, “Teacher, why is there no oneths?” The teacher posed this question for discussion in class, encouraging students to offer explanations. While two students argued that oneths exist, a few other students presented counter-arguments. The teacher emphasized some student utterances by posing questions, such as, (a) If oneths existed, what would it mean? (b) If oneths is not a fraction, where would its position be in a decimal number? and (c) Are ones and oneths different? The teacher together with the students discovered why oneths does not exist while emphasizing the relation between place values (refer Takker & Subramaniam, 2019 for details).
Concluding thoughts
The students’ question about oneths was not anticipated by the teacher and its potential was undiscovered in the earlier lessons. When the teacher decided to discuss the question, she used the key idea of place value in a base 10 system. Sometimes as teachers, we ignore students’ questions, may postpone them, or even forget them. However, we can also consider students’ questions as opportunities to communicate key mathematical ideas. Resources such as textbooks, research literature on students’ topic-specific conceptions#, discussions with colleagues and the students themselves are useful in handling such situations. Listening to such student ideas and responding to them in ways which are productive to developing students’ mathematical thinking is challenging, yet a valuable goal of mathematics teaching.
References
- Ball, D. L., Hill, H. H., & Bass, H. (2005). Knowing mathematics for teaching: Who knows mathematics well enough to teach third grade, and how can we decide? American Educator, 29(3),14-46.
- MacDonald, A. (2008). ‘But what about the oneths?’: A Year 7 student’s misconception about decimal place value. Australian Mathematics Teacher, 64(4), 12-15.
- Takker, S., & Subramaniam, K. (2019). Knowledge demands in teaching decimal numbers. Journal of Mathematics Teacher Education, 22(3), 257-280.
*What would have led the student to ask this question? How is the decimal interpretation helpful in understanding the use of this unit?
#Probing and analying students’ responses is an important way of developing such knowledge. For more details, refer to, Takker, S. (2019). Understanding learners’ thinking through an analysis of errors. At Right Angles, Azim Premji University.
The author is pursuing her PhD in mathematics education from the Homi Bhabha Centre for Science Education, TIFR, Mumbai. Her doctoral research is on developing teachers’ knowledge of students’ mathematical thinking by supporting them in the contexts of their practice. Prior to pursuing her PhD, she worked as an elementary school mathematics teacher. She can be reached at shikha@hbcse.tifr.res.in.
