Sanjeev Ranganathan
Forty years ago Seymour Papert (mathematician and a pioneer of programming) commented, “Is the child programming the computer or is the computer being used to program the child?” Technology in education has come a long way since then. In this article I look at how children learn (in this case, mathematics) when they use computer programs.
The case studies cited here mostly use Scratch (a programming language for children) and are based on the work at C3STREAM Land (Science, Technology, Research, Engineering, Arts, Mathematics), rural resource centers around Auroville, a universal township dedicated to human unity. The children coming to these centers from Auroville and surrounding villages are provided access to puzzles, games, programming, robotics and various mathematical materials.
As a pattern identifier
Children can program the computer to simulate a thought pattern and easily spot patterns they couldn’t before.
Pooja (8th grade) is learning cubes and cube roots; she often mistakes x3 (x multiplied by itself three times) with 3x (x multiplied by three). In an attempt to help her deal with and understand large numbers I suggest that she can guess the cube roots of large perfect cubes (e.g., 830,584) by estimating how big a number is (how many 1000s) and looking at its unit digit. I hope this will help her get a sense of numbers. But she is unable to follow the procedure and finds the going tough (she is not alone in this).
She then starts developing a program to find the cube roots of numbers. Her initial goal is to print the first 10 cubes. Power is not an available expression and she needs to construct the expression for a number (variable). In time she creates result = number × number × number. She increases the number each time and puts it in a loop. To view the results, I ask her to put in a delay of 1 second after each calculation. I ask her to notice the numbers, but she still doesn’t find the pattern.
She then changes the loop condition to keep it running till the result is a large cube given in her book. She now becomes interested in where the program stops and intently looks at the results. She soon figures out when she is too far and needs to wait for the result and asks to reduce the time between calculations.
I tell her she could change the program and have fewer calculations, but retain the time after a calculation to see the result. She decides to skip numbers in her program. I connect this to the original process and ask her to change in steps of 10 (10, 20, 30, etc.) till the result is too large, go to the previous step and then go in steps of 1.
She implements this as two loops: first loop in steps of 10 and the second in steps of 1. It takes her time and she makes errors, but she understands what she is trying to do and debugs it with known cube numbers and their cube roots. To use the program she generates a random two-digit number (a feature available in Scratch) and uses its cube as the target (variable). This time when she looks at the steps of 10 she notices that the last three digits are 0s. She then notices that the non-zero digits have the same pattern as cubes of single-digit numbers. When the second loop starts, the numbers are much more complicated. I ask her to focus on the units place. Now, she notices a pattern-1 in the units gives 1 in the units of the cube (213 = 9261). Similarly, 4 gives 4, 5 gives 5, 6 gives 6, 9 gives 9. For the other digits between 1 and 9, she notices that 3 flips with 7 (433 = 79507 and 573=185193) and 2 with 8. She starts working this out systematically as the computer does and now she gets it. In time she skips the ‘unnecessary’ steps and gets straight to the cube of the 10s and then writes the number including the units. She makes the program a game that accepts inputs to check her answer. The program still works through all the steps for her to crosscheck her thought process and then announces the result. In the next class she works out 50 cube roots in an hour in her notebook and checks with the computer. She gets one wrong and understands why that one confused her.
Not only does Pooja use the computer to identify a pattern she was unable to see, she also uses it to get a sense of numbers, thinking logically while learning a procedural skill and developing an understanding of the concept. We also notice that in the process of creation, the learning becomes her own. This is the aspect emphasized in the constructionist paradigm.
As a way to look at scaled down problems
A few children from 10th grade design a physical game of Venn diagrams for three sets. Each circle in the Venn diagram represents a set constructed by a rule. There are three rules – one for colour, one for shape and one for size. In each rule there are three choices. The rule for colour can be red, green or blue. The rule for shape can be triangle, square or circle. The rule for size can be small, medium or large. The goal is to guess the rules of each set in a minimum number of chances.
This physical game inspired Diva, a 9th, grader to make an interactive game in Scratch with the computer choosing a rule randomly. This required Diva to break the big game that was too complex into a smaller game with two sets. Diva also realized that in order for the computer to understand which region of the Venn diagram was being accessed, he needed to divide the Venn diagram (for 2 circles) into A-B (in A and not in B), B-A, A∩B (in A and B), and U-AUB (outside the two circles).
Even though visually it looked like a single picture it was in fact composed of four different pictures (or sprites). This also helped him understand the different regions of the Venn diagram better. A snapshot of the game in action is shown in Figure 1.
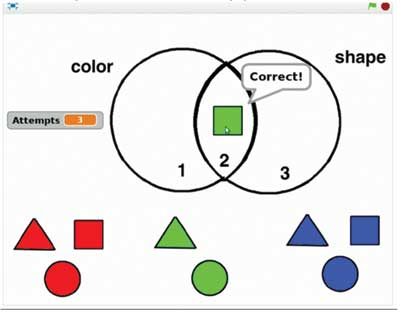
Diva first made the game with fixed rules which did not interest him much so he wrote out a program that allowed the computer to randomly pick the rules. This made the game challenging for him too.
Creating games like these not only help children understand concepts better, but they also push children to learn more. Just as Diva had been inspired by a game made by others, 8th graders were inspired by Diva’s game, wanted to understand how it works and learn about sets even though they did not have it in their syllabus yet. At C3STREAM Land we have sessions where children share their projects once a week to encourage such learning.
Unleashing creativity using art for expression
The children who come to C3STREAM Land make many projects to demonstrate their learning and use these as presentations for other children to learn concepts. Some of these are remarkably detailed and artistic. A child working on coordinate geometry decided to create an interactive game that allowed the user to enter points one-by-one to form a picture, which when completed became a van as shown in Figure 2.
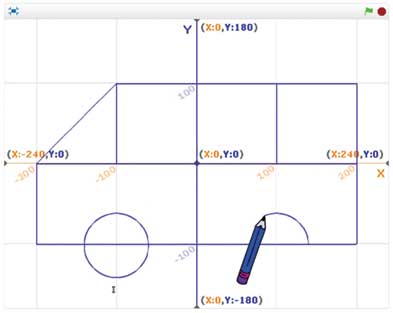
These projects add a very important element of creativity and beauty and inspire the group as a whole to want to create not just projects, but beautiful projects. It also adds the generally missing element of art to mathematics making learning mathematics all the more joyful.
Getting a sense of variables
“Viewing” an expression, e.g. (x+y)2, as a geometric shape is being encouraged in textbooks in Tamil Nadu as a way of concretizing abstract concepts as squares (x2 and y2) and rectangles (2xy). These images are usually static in the textbook, but when children create a program for demonstrating this and vary the values of x and y there is a good chance that they will get a sense of the variables and connect it to what they use in programming.
Connect with the real world
Programming hardware allows children to connect with the real world and motivates them to complete a project as they develop problem solving, logical thinking skills and bring these aspects to something they care about. Over the years, the children have made different projects with Arduino (an open source prototyping platform used for building electronic projects) including a school bell, a clock, a display of C3STREAM Land, a water overflow alarm for ground water, a robot that moves things from place to place, etc.
I would like to tell you about a project where a child was having fun creating a two digit clock (measuring seconds) with the seven segment display (a form of electronic display device for displaying decimal numerals).
A couple of the letters in the C3STREAM Land display made by the children a year ago were not blinking properly. Two children in the 7th grade expressed interest in fixing the display. A facilitator walked them through how powering one leg of the display can light up one of the seven segments similar to an LED (Light Emitting Diode). They quickly grasped the idea and fixed the display in a couple of classes. After fixing the display one of the two students was interested in doing something more with Arduino. He wired up the seven segments to different Arduino pins to control the segments individually and managed to write his first program in ‘C’ to display the number ‘1’ by the end of the class. Using his understanding of blocks in Scratch he extrapolated how he could clear the numbers and change them. He needed some help getting around syntax errors during compiling ‘C’ programs, but then worked on his own for 45 minutes. In this time, he had made a single digit counter that increased from 1 to 9 every second. He then asked for ideas on extending the functionality to make a clock using Arduino. After talking to a facilitator, he added a second seven segment display to get the second digit of the clock. He even managed to figure out the logic of the first digit continuing to run when the second was implemented to create a 99s counter on his own.
Programming can be an active way to challenge middle school children to find ways to demonstrate their knowledge in mathematics and learn something deeper as well along the way.
The author is the recipient of the Lewis Winner award and has built over a billion products as an engineer. He moved to Auroville seven years ago and started working with rural children and youth. He set up C3STREAM Land, a centre where children come to learn mathematics, programming, electronics, leadership and much more. He can be reached at sanjeev.ranganathan@gmail.com. To know more about his learning centre and its work visit www.auraauro.com.