Stacking everyday liquids
Megha Chougule and Adithi Muralidhar
Introduction
Have you ever tried stacking liquids on top of each other? Sounds impossible? Remember seeing motor oil floating on top of water puddles during monsoons? How about an oil spill/slick, where you see oil floating on top of the water in the sea? While cooking food, the oil tends to float on top of the watery broth. These are the most common examples we see from everyday life, yet the thought of stacking liquids does seem counter-intuitive. The following activity is a fun way to introduce students in upper primary classes to the concept of density.
Objective
To introduce the concept of density in liquids.
Materials required
• Test tubes
• Test tube stand
• Pipette/droppers
• Honey (yellow colour)
• Dish-washing liquid (green)
• Water (add blue food colouring agent)
• Hair oil (red colour; you also get other coloured hair oils in the market)
• Laboratory alcohol (no colour, transparent)
• Lab weighing scales
Present the colour puzzle to students
The five liquids chosen for this activity are everyday liquids that students will be aware of. Apart from laboratory alcohol, all other liquids are likely to be found in their homes. Each of the chosen liquids has a different colour. Prepare a set of 6 test tubes (capacity 10-20ml) as shown in the diagram below:
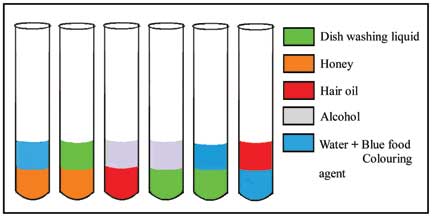
Preliminary questions for students: Observe the given test tubes carefully. How many different liquids are present in the test tubes? Can you guess what each of the (everyday) liquids could be?
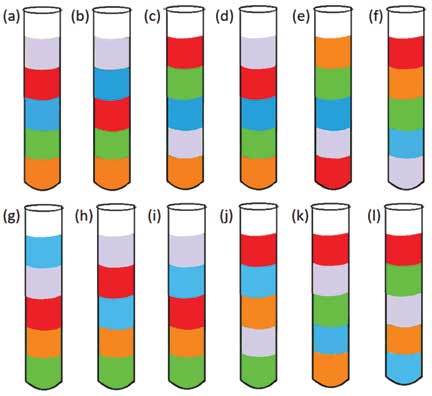
Predict: What is likely to happen if all the liquids are put in one test-tube? If we add equal volumes of liquids, what will be the order of stacking?
Perform and observe: If you have predicted the order of liquids, start making your liquid column by adding the different liquids into the same test tube as per your prediction. Add equal volumes, i.e., equal millilitres (ml) of liquids using a dropper or a pipette and check if the outcome matches with your prediction or not.
Explain: With younger groups of children, you can provide a chart with various possibilities. You can call groups of students to argue for or against the possibility of each option. For example, if students say that option (j) is the wrong answer, ask them to defend their stance. Get them to communicate with the rest of the class, why option (j) is perhaps incorrect. Students may find this a fun game.
Extending the activity
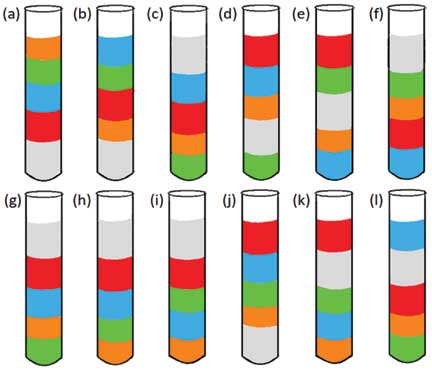
Predict: If you add equal masses of the five liquids, what will the order of stacking be?
Perform and observe: If you have predicted the order of liquids, start making your liquid columns. Add equal weights, i.e., equal grams (g) of liquids to a test tube (preferably each liquid should be greater than or equal to 2g) and check if the outcome matches with your prediction or not.
Explain: With younger groups of children, you can provide a chart with various possibilities and have them explain their observations.
How does this liquid stacking happen? What determines the stacking order?
Stacking happens when liquids are immiscible, i.e., when the force of attraction between the molecules of the same liquid is greater than the force of attraction between the molecules of two different liquids. Liquids taken in this activity are immiscible. Thus, when you add all five liquids, they stack up.

Ask students to observe the column with equal volumes (column I) and the column with equal masses (column II) [Refer Figure]. In column I, the volume of all five liquids is same and mass is varying. In column II, mass of all the liquids is same and volume is varying. From these two figures we can clearly see that the stacking order in both columns is same irrespective of how much each liquid weighs (mass) or how much space it takes up (volume). Thus, mass and volume aren’t independently determining the stacking order.
Let us see if ‘density’, a measure of how tightly a substance is packed, is related to the stacking order. Density is calculated as the ratio of mass to volume, i.e., D = M/V. Therefore, it follows that mass to volume ratio will be high if the substance is tightly packed and it will be low if the substance is loosely packed.
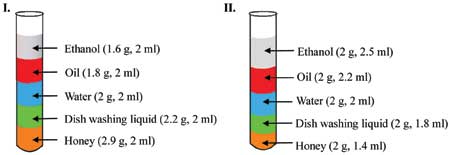
Ask students to calculate M/V value of each liquid in column I and II. They will find out that different liquids have different mass to volume ratio (e.g M/V of honey = 1.4 g/ml, M/V of water = 1 g/ml, etc). However, mass to volume ratio of the same liquid in columns I and II is same (e.g. M/V for honey in column I and II is the same, i.e., 1.4 g/ml). Ask students to observe how the liquids are stacked in column I and II keeping in mind the density values. They will notice that the liquids in both columns are arranged in ascending order of density (from top to bottom). This indicates that the mass to volume ratio (density) determines the stacking order!
The density of a substance remains the same regardless of how much it weighs and how much space it occupies (at a given temperature and pressure). When immiscible liquids are mixed, the liquid with lower density floats and the liquid with higher density sinks.
This activity was carried out with children in a large age group (grade 5 to 12) as it was conducted during an Open Day.
Is there an alternative to test tubes?
We can also stack the liquids in everyday household items like transparent glass mugs, empty pocket sanitizer bottles, empty nail-polish remover bottles (where the sides of the bottle are straight, not slanted) etc. However we will need six exact replicas to make the set of six. And more quantity of each liquid, if you plan to use something as large as a glass mug.
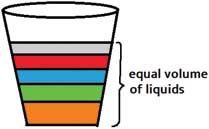
We have tried stacking liquids in water glasses. However, the problem is that most of the glasses do not have sides that are straight. In glasses where the sides are slanted, when you take equal volumes of the liquids, the height of each layer is different (as shown in the figure). That is, even though liquids occupy equal space, their heights are different. (In spite of equal volumes, there is no symmetry). And this can be a little confusing when children are doing this activity.
Thus, small bottles with straight sides can be a desired alternative.
Acknowledgments: We acknowledge the support of the Department of Atomic Energy, Govt. of India, under Project Identification No. RTI4001.
References
• https://www.scientificamerican.com/article/stacking-liquids/
• https://extension.purdue.edu/4h/Documents/Volunteer%20Resources/Science%20Made%20Easy/7Layer%20Density%20Column.pdf
• https://www.ccsdut.org/site/handlers/filedownload.ashx?moduleinstanceid=617&dataid=3456&FileName=s2liquid%20layers%20worksheet%20reg.pdf
• https://www.exploratorium.edu/snacks/klutz-proof-density-column
• https://www.homesciencetools.com/a/liquid-density-project
• Adebayo, F. (2015). Generative and Predict-Observe-Explain Instructional Strategies: Towards Enhancing Basic Science Practical Skills of Lower Primary School Pupils. International Journal of Elementary Education, 4(4), 86. doi:10.11648/j.ijeedu.20150404.12
The authors work at the Homi Bhabha Centre for Science Education, TIFR, Mumbai. They can be reached at meghac@hbcse.tifr.res.in.
