Monica Kochar
Probability is a very interesting topic for it deals with ‘chance’. How likely is it that it will rain today? Are you certain or uncertain about this movie? Is it impossible for me to climb the Everest? Possibly I am going to grow my hair. It is certain that tomorrow is a holiday. Events in our lives move between “certain-likely-possible-unlikely-impossible”.
To teach ‘probability’ to students without bringing in the fun experiments would be quite criminal. Here is a fun experiment you can bring in your class when this topic is discussed.
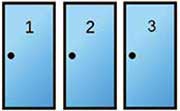
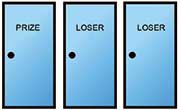
This problem originates in a television show called “Let’s make a deal” run by the host Monty in 1963 in USA. In the problem you have three closed doors. One door conceals a Prize (like a car) and the other doors hide two identical loser-prizes (like two goats). The contestant selects one of the doors. Monty opens one of the other doors, revealing one of the goats. The contestant then must decide whether to stick with the first selection or to switch to the other unopened door. What should the contestant do?
Note
• Monty will only open doors that do not have the prize behind them.
• Monty will never open the door that you chose.
Most people say it doesn’t’ matter whether you switch your choice or not because – the probability of each door being a winner is 1/3rd, and once one door has been opened, the probability of each closed door being a winner is 1/2.
But it does matter!
Suppose you’re on the game show and you’re given the choice of three doors. Behind one door is a car; behind the others, goats. You get only one chance to choose the door and one chance to switch/not switch! You have three choices – doors 1, 2 or 3.
There are only three ways this game can go!
Option 1 – The car is behind door 3
Let us make a table to see what happens with each choice if you switch or do not switch.
| The door you choose | The door Monty opens | Effect of switching | Effect of not switching |
| 3 | 1 or 2 | Lose | Win |
| 2 | 1 | Win | Lose |
| 1 | 2 | Win | Lose |
Note that the probability of winning is 2/3rd if you switch the door and 1/3rd if you do not.
Option 2 – The car is behind door 2
Let us make a table to see what happens with each choice if you switch or do not switch.
| The door you choose | The door Monty opens | Effect of switching | Effect of not switching |
| 3 | 1 | Win | Lose |
| 2 | 1 or 3 | Lose | Win |
| 1 | 3 | Win | Lose |
Note that the probability of winning is 2/3rd if you switch the door and 1/3rd if you do not.
Option 3 – The car is behind door 1
Let us make a table to see what happens with each choice if you switch or do not switch.
| The door you choose | The door Monty opens | Effect of switching | Effect of not switching |
| 3 | 2 | Win | Lose |
| 2 | 3 | Win | Lose |
| 1 | 2 or 3 | Lose | Win |
Note that the probability of winning is 2/3rd if you switch the door and 1/3rd if you do not.
In all cases, the probability of winning is higher if you switch.
Presenting the problem in class
Keep aside one lesson after the topic has been covered for the students to play a game that is based on this problem. It will be fun, they will learn to develop a strategy and also find ways to apply the strategy.
Homework before the lesson
a. Ask students to make “Monty hall” type cards from home and bring to school.
b. Make two sets of three cards each. All six cards to be of the same shape and size.
c. Set 1 – The 3 doors
d. Set 2 – The 3 prizes (1 winner and 2 losers)
e. Let the students choose their own sets of prizes.
Class work on the day of the activity
Share with your students the Monty Hall problem without giving out the solution. Ask them to play the game and check the solution. Reveal the solution only in the end – that is ‘in switching there is a greater probability of winning the game’.
The game
- Each student plays with one partner.
- One partner is the host and the other one the contestant.
- The host organizes his cards on the table with numbered cards on top and the ‘prize’ cards below them. He knows behind which numbered card the prize card is.
- The contestant chooses a card.
- The host opens another card that does not have the prize beneath it.
- The contestant chooses to switch or not switch and selects his final card.
- The host decides if the contestant won the prize or not.
- This completes round one.
- The players swap positions and play round two.
- The players play a total of 10 rounds deciding in each round if they want to switch or not.
- A record is kept on the table that keeps a tally of the number of wins/loses, when switched or not switched.
- The players total in the end the number of wins when switched or not switched and find the probability of winning when switched or not switched.
Record sheet
| Round | Switching | Not switching |
| 1 | I won/I lost | I won/I lost |
| 2 | I won/I lost | I won/I lost |
| 3 | I won/I lost | I won/I lost |
| 4 | I won/I lost | I won/I lost |
| 5 | I won/I lost | I won/I lost |
| 6 | I won/I lost | I won/I lost |
| 7 | I won/I lost | I won/I lost |
| 8 | I won/I lost | I won/I lost |
| 9 | I won/I lost | I won/I lost |
| 10 | I won/I lost | I won/I lost |
| Total | Number of wins = ….. | Number of wins = ….. |
| Probability of wins |
Is the probability of winning higher when you switch or not switch? What did you discover?
Resources
- A web-link to play this game online: http://math.ucsd.edu/~crypto/Monty/monty.html. You can not only play the game here but also test out the results of hundreds of other players. Their data shows clearly that switching is more beneficial!
- A YouTube link for solution: https://www.youtube.com/watch?v=maY41UPKiXs.
- A good explanation is given at: http://geardiary.com/2013/01/10/random-cool-math-fact-the-monty-hall-probability-problem/.
The author has taught math for 19 years in Indian and international schools. All through her teaching career she was known as a very creative math teacher who helped students get over their math phobia. Currently she works with teachers to kindle the same fire through her sessions in math, exploring the self and CCE. She also works as a curriculum developer and mentor for math curriculum. She can be contacted at reachmonica@gmail.com. She also has a facebook page www.facebook.com/humanemath.