B S Shylaja
The title perhaps reminds one of the famous golden ratio; the ratio that determines the most pleasing aspect ratio for a post card, a greeting card, posters or a simple visiting card. There are many more ideas from mathematics that have defined aesthetics from ancient times.
When I was a child I remember my seniors posing a puzzle to our class that involved transporting a cow, a tiger and a bag of fodder for the cow across the river. I will change the components so that you will not be bothered by clever questions from your students (How can you transport a tiger? Was the cow not scared? The tiger can swim … and so on, questions that we never thought of asking at the time).
So, here is a farmer with a dog, a hen and a bag of grains. He has to cross the stream with a boat which can carry only two items at a time. Of course, one is the farmer himself because he has to row the boat. Suppose he takes the dog first, the hen will tear the bag to eat the grains. Suppose he takes the bag of grains, the dog will kill the hen. So how will he manage? He is allowed to make any number of trips so that he will leave one item on the other bank and return to pick the others.
I hope you have successfully figured out the answer without much effort. Such exercises can be used to teach “permutations and combinations”. It is not just in the classroom but this kind of thinking is being employed in the manufacturing of combination locks, allocation of telephone numbers and vehicle registration numbers and even in the generation of automatic passwords.
It is interesting to note that it is not just our new textbooks but even the (really) old texts of Bhāskarāchārya and Mahāvirāchārya discuss derivation as we learn it today and provide practical examples. One example concerns the arrangement of letters in an order called Candas, translated as meter.
Let us address a problem faced by sculptors. The sculptors were approached by temple trustees wanting an idol either of Keśava or Janārdana or Narayana. All are different names of Vișnu, but the sculptor has been taught that each of these idols has to be made according to the given rules. The idol has four hands, each of which carries a different item – Śankha, Cakra, Gadā and Padma. The name specifies the items that should go in each hand. For example, Keśava has Padma in the lower left hand, Śankha in the upper left hand and Chakra in the upper right hand (the remaining item in the fourth is understood). Narayana will have Śankha in the lower left hand, Padma in the upper left hand and Gadā in the upper right hand. The list is available in many texts devoted to iconography. Given this how many such idols are possible?
This is a simple problem that can be solved using “permutations and combinations”. There are four items (A B C and D) and four places (a b c and d). Staring with (Aa Bb Cc and Dd), (Ab Ba Cc and Dd) etc., we get 24 possibilities. If we start writing down all the possibilities it will fill multiple pages and each time we want to look up one possible combination we will have to refer to every single page. So how did the sculptors manage to remember this order? That too for centuries? The clue comes from the fact that the same rules are applicable all over India.
This secret was uncovered by Prof. S R Sarma, a veteran historian of mathematics and astronomy. He brought to light a book by the name Manasollāsa written in the 11th century which has a verse set in proper meter (Chandas) and can be memorized. It is coded very elegantly giving the first letter of the three objects in the order of lower left, upper left and upper right. The first phrase is paśachanke means pa (Padma) sha (Śankha) cha (Chakra) and the fourth syllable is for the name ke (Keśava). You can appreciate the cleverness in just specifying three to match the meter since what has been left out is obviously the fourth item. The second example is the phrase śapangana – sha (Śankha) pa (Padma) ga (gadā) and na (Nārāyana) and so on. Here is the verse reproduced from the work of S R Sarma and the list.

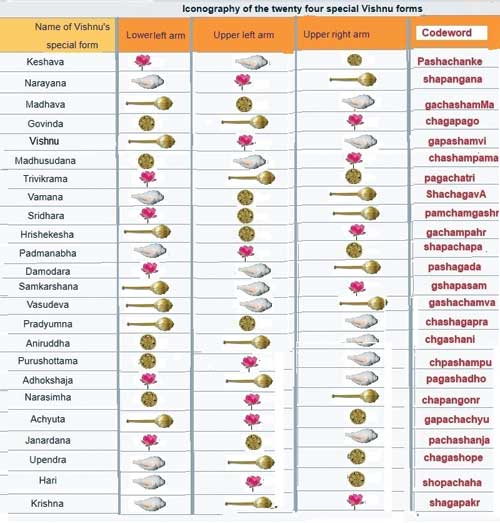
However, one may naturally think that there should have been one standard depiction of all the 24 somewhere as a reference like a textbook. When the sculptors had the time, money and freedom to execute such a task, they did it. A small village called Nuggehalli, which is very close to Beluru, with the temple famous for its sculptures (in Hassan district of Karnataka and a well-connected tourist destination), houses all the 24 statues in the same order as depicted in the verse.
Let us now see an interesting application of the same in Indian music. In all ragas we have seven notes (svara). It is well-established that the names of the rāgās have been coined so as to represent the serial number. The melody of the rāga is governed by the choice and rendering of the svarās and musicians excel at this. The rāgās are derived from the same seven notes with all possible combinations. Yes, but how many?
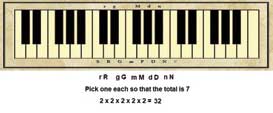
It is mandatory that a Sampūrņa rāga should have sa (Şadja) and pa (pancama). Then we are left with the other five to be chosen. A definite set of ratios are selected in fixing the other notes. Ŗșabha, Gāndhāra, Madhyama, Dhaivata and Nișāda are the names given. As shown in the figure, two Ŗșabhas are possible represented by R and r; two Gāndhāras are possible G and g; similarly M and m, D and d, N and n are marked. Let us attempt the combinations:
SRGMDN can be one rāga
SrGMDN can be another
SRgMDN
SrgMDN… and so on.
So how many ragas are possible? We need to pick one each from the two possible notes for R, G, M, D and N. That makes it 2 x 2 x 2 x 2 x 2 = 32. Therefore, we expect that there should only be 32 Sampūrņa rāgās.
Yes, that was indeed the case. There are several references to 32 rāgas in the Hindustani system. Dr Sukanyā Prabhākar, a well-known musician, has studied the old texts and found that this system of 32 was prevalent till about the 15th or 16th century. We find references to that in the compositions of the great saints Nijaguna Śivayogi and Purandara dāsa. However, the identification of 32 rāgas appears to differ over centuries.
There is another option possible. We can consider three options for R and D. Essentially, R can have R, r and R’. Here R’ is the same as G. Similarly D can have D, d and D’ where D’ is the same as N. So the new rāgas can be
SR’gMDN and
SR’gMD’n and other combinations.
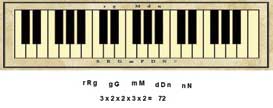
This gives us a total of 3 x 2 x 2 x 3 x 2 = 72 rāgas. This system of melakartās is very well known today. All the combinations result in melodious compositions and are quite popular. The subdivisions into 12 chakras are also standardized.
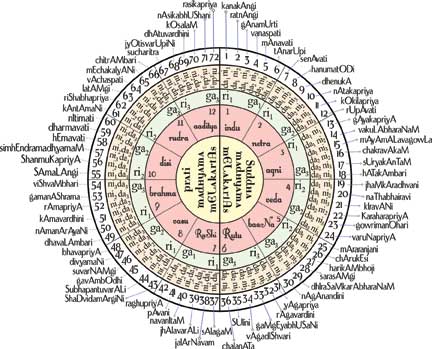
(Image courtesy: Basvarajtalvar: https://upload.wikimedia.org/wikipedia/commons/0/0e/Melakarta.katapayadi.sankhya.72.png)
Here we discussed two examples of application of permutations and combinations in an apparently unconnected field. If we look at nature which has an amazing variety of biological and plant species, we are sure to find more examples – maybe in the patterns of leaves or sequencing of proteins.
 Bhāskarāchārya poses a very interesting problem in Lilāvati, assuming that everyone knows that there are 24 forms of Vishnu. It reads like this (from S R Sarma)
Bhāskarāchārya poses a very interesting problem in Lilāvati, assuming that everyone knows that there are 24 forms of Vishnu. It reads like this (from S R Sarma)
Just as in the case of Vișnu, can you figure out how many forms of Śambhu are possible? He has 10 hands and 10 emblems.
An interesting application of permutations and combinations can be seen in a text of Jaina philosophy. There are 15 kinds of pramādās defined; pramādā can be roughly translated as carelessness or mistake or an offence. There are five subdivisions with unequal distribution; they are vikathā (wrong talk, 4), kāșāya (passion, 4), indriyā (sense, 5), nidrā (sleep, 1) and praņayā (attachment, 1). Combinations of five are made taking one from each category. The Jaina philosopher Nemi Chandra of the 10th century has laid down the rules and provided serial numbers also for them. How many such combinations of offences are possible? It is simply 4 x 4 x 5 x 1 x 1 = 80. The allocation of the serial number also is quite intriguing; one may read it from his work “Gommatasāra”.
The author specializes in observational astrophysics. After obtaining a PhD on hot binary stars, she continued research on comets, peculiar stars and infrared astronomy before joining the Planetarium at Bengaluru. She has been working in the area of history of astronomy using unconventional records of stone inscriptions. She can be reached at shylaja@taralaya.org.
