Vijay Anand
I was into my third month of teaching science and mathematics to middle school, when an email popped up in my inbox inviting articles for a journal. Settling into a new career and managing my personal expectations was taking a lot of time. While the email remained in the inbox, albeit with a flag, the impending deadline was playing on my mind. I was preparing for an ultra marathon and the procrastination was building up the stress level with many agenda points in my diary and my mind. On a lovely morning, while I was making the rounds of the sports field during a practice run, the idea suddenly struck me: ‘How about writing an article on the use of mental mathematics in running and the pedagogy of teaching mathematics using the methods I followed to keep my mind engaged during my long, meditative runs?’ With that spark in my mind, I sat down to write this article.
My best thoughts come to me while I am running. It is important to keep your mind active and alive during these long runs, and so I would juggle all the numbers in kilometres, minutes and hours and fractions of these. During the training, one needs to do various speeds and distances in a week, which are usually planned in advance. While doing a paced run, I would keep my mind sharp with questions such as, “Can I cover the balance distance in the time available?”, “At what pace will I need to power myself to complete the target distance in the available time?”, “If I drop my pace on an upslope, what should be my pace downslope to maintain the average pace?”
Now, here lies a wonderful opportunity for me to use these basic calculations from my real runs in the very real world to initiate mental mathematics to my students gradually. For the beginners, it would also serve as the “talk test” – if a runner is able to talk in a flow, it would mean that he or she is comfortable. If the talk is in spurts, that shows the degree of discomfort the runner is in. The quality of the answer itself would indicate the amount of concentration invested by the runner in calculating while running. My school has an athletics track and running on that has its own advantages. When an opportunity showed up on a run with the kids during the sports period, I would ask, “What fraction of our intended distance have we covered?”, “What fraction is yet to be completed?”, “How many more laps before I complete my target distance?”

Using the standard distance of the track known to them, they could practice the unitary method and answer elementary questions. It would be more (or less) than the 400m length of the track, and so the opportunity to exercise the mathematical mind arises here when the distance is changed in notches of ‘5’ or ‘10’ metres for further practice. “If we have run three rounds (assuming all rounds were covered on the same path outside the track) and have covered 2km, what distance is each round? If we need to cover one more kilometre, how many more loops would be required to be completed? Will it be a complete loop or a fraction of a loop?” Besides, running on a track doing endless loops builds mental strength. The next stage would be to take them off the track. Now the standard distance would not be evident as we move on to a non-standard distance of the unmeasured trail.
Using the measurements made each day (on my smart watch) of the different sections of trails and the combinations of their distances, linear equations could be introduced and solved in a very practical manner.
Furthermore, the time available for the bell to go off for the sports period and the target distance pose unique opportunities to calculate the pace required to meet these two constraints. The training schedule can be tailored to ensure that mathematics fit in properly to exercise mind and body together.
Running on the roads gives a different mathematical perspective besides giving a refreshing break from the monotony of the campus.
For example, take three different routes on three days, each having an overlap with a section of the other two (or even one) routes. Assuming that you know only the total distances covered on each day (meaning you don’t know the lengths of each section), linear equations could be set up to find the distances of each section. An unknown distance can be found using the known distances of segments of a route during previous runs.
Another advantage running brings up in moulding the mathematical mind is that it allows the practice of “estimation”. The art of estimation is an important quality in both running and mathematics. While running, a constant question on the mind is, “How much more to go?”, “Am I nearly there yet?”. While doing this, the picture of the familiar route (if one travels that route often) allows one to guess the distance to go before you reach the destination. Estimation usually starts with a rough guess. Then using previous knowledge of travels on the same route, or even known standard distances or lengths (like the distance between two poles), the rough estimation can be narrowed down to a more accurate distance. For example, before starting a sprint across the sports field, the runners may be asked to guess the distance to a tree designated as the finish point. The estimate could then be narrowed to a more accurate guess using the standard distances available on the field (like the distance between the goal posts of a football ground). After the initial guess from the runners, another question, “How many football fields would fit in between us and the tree?” may be posed to them.
This would evoke a refined ‘guesstimate’ from the students/runners. Finally, the distance could be measured on foot to a more exact value.
How does this fit into classroom mathematics? Estimation by comparison allows two things. At first, the inertia in starting the train of thought would be overcome due to the inquisitiveness to find out the answer to the question, “Is my guess correct?” Then, over a period, the art of weighing the benefits while using multiple known formulas and methods will gradually sharpen the ‘inquisitive’ mind to develop a sixth sense of appropriateness of a formula or method for solving a mathematical problem quickly.
Another important quality common to both runners and mathematicians is “perseverance” that these disciplines demand. If one has the ability to fill the unforgiving minute with 60 seconds worth of distance run, that quality will take the runner farther in mathematics too.
Mathematics demands certain qualities of the mind that do not allow it to wander away from seeking the solution persistently. The elusive solution to certain mathematical problems can only be solved if approached cautiously and persistently. It is also a well-established fact that hard work and concentration are synonymous with good skills in mathematics. Running demands these qualities too and hence goes very well in imbibing qualities required for good mathematical skills. Finally, the good feeling or the “runner’s high” experienced after a good run is comparable to the feeling obtained after finding the elusive solution to a mathematical problem.
Using simple mental calculations during physical activities, it becomes easier to demonstrate to students that mathematics need not be learnt just through writings on classroom boards or homework books and more importantly, that mathematics has everyday utility. And what better way to learn it than while running which accrues physical and psychological benefits?
Activity
A person’s running route has been constantly the same. His running routes on 3 different days are as follows:
Day 1: On day 1, the person just ran up to the field and sat down on a bench watching the morning birds.
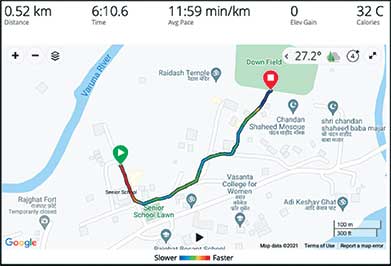
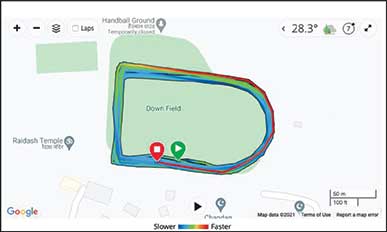
Day 2: On day 2, he only took 21 laps/rounds of the field, but he forgot to switch on his watch that measures the distance and hence did not know the exact distance.
Day 3: On Day 3, he ran up to the field through the same route and ran 8 and 1/4 rounds of the field.
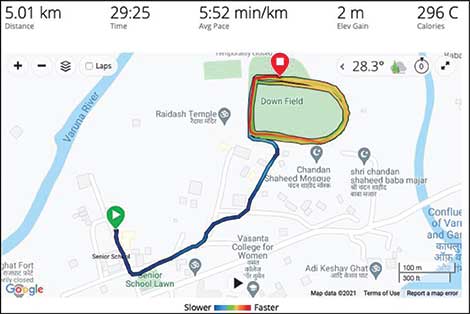
How much did he run on the second day?
Write a system of equations for the problem and solve it.
The author is a teacher at Rajghat Besant School, Varanasi, and you can read more about him at
https://www.rajghatbesantschool.org/getinvolved/the-team. He can be reached at nv_andy@yahoo.com.
