M. Gopalakrishnan
There is no one way to look at a problem. One doesn’t gain complete understanding by solving a problem in just one way. A problem can be solved in many different ways. Once a student solves a problem in one way, she tends to move to the next problem and doesn’t pause to think whether there is another way to solve the same problem. Trying to solve the same problem in many different ways will deepen one’s understanding of the problem. I try to encourage this in my classes.
After explaining the midpoint theorem to class 9 students, I gave them a few simple problems involving triangles to help them understand the concept better. They solved the problems using the midpoint theorem. Then I gave them the following problem and asked them to solve it, assuming that they would solve it by applying the same theorem.
Q1: ABCD is a rectangle. P, Q, R and S are midpoints of the sides in order. Prove that the quadrilateral PQRS is a rhombus. (Fig-1)
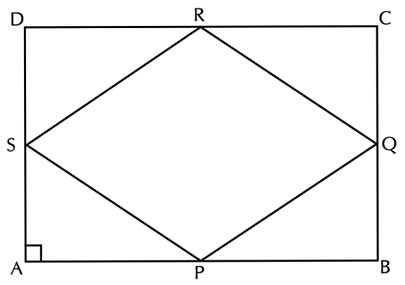
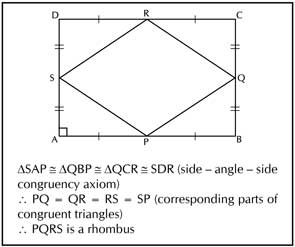
After a few minutes, Vinaya (all names have been changed) approached me and asked, “Bhaiya, is it necessary that we use only the midpoint theorem for solving this problem?” Though I wanted them to use the midpoint theorem in order to practice it, I told her “No. There is no such requirement. You can use any other concept you know already. Only make sure that your reasoning is correct.” She took some time, identified the four congruent triangles using the side-angle-side axiom and solved it as shown in Fig-2.
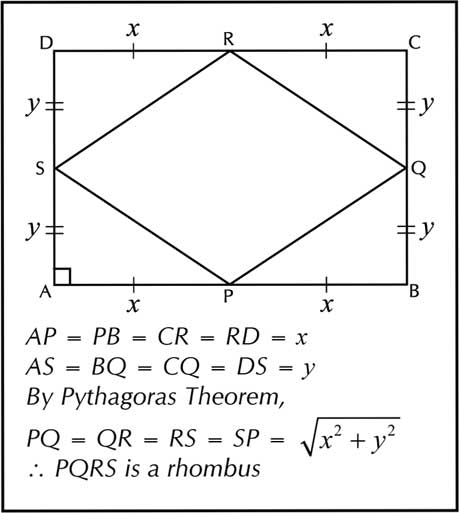
I was impressed. I asked the class whether anyone else could think of a different solution. Arpit saw the four right triangles and hit upon the idea of using the Pythagoras theorem. (Fig-3) I was even more impressed. I appreciated both of them and shared their solutions with the entire class.
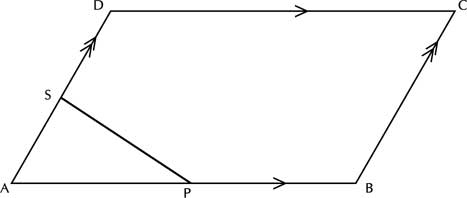
Later I asked them whether they could solve the same problem using the midpoint theorem. Students spent some time and figured out that by drawing a diagonal, the rectangle could be divided into two triangles. (Fig-4)

This made me realize how creative students could get in coming up with different solutions to the same problem. On another occasion, I gave them the following problem:
Q2: ABCD is a parallelogram. P and S are midpoints of AB and AD respectively.
Prove that area APS = 1/8 area ABCD (Fig-5)
You may try to solve and see how many different solutions you can come up with. My students came up with four different solutions.
For the following problem they came up with three different solutions:
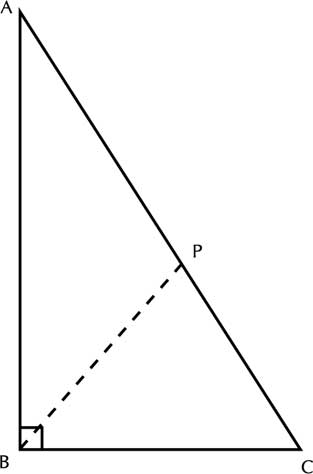
Q3: Triangle ABC is right angled at B. P is the midpoint of AC.
Prove that PA = PB = PC (Fig-6)
Conclusion
While teaching any concept, students should be asked to solve a problem in as many different ways as possible, including the application of the recent concept taught. This motivates them a lot, makes them look at the same problem from different perspectives, strengthens their understanding and helps them be creative.
The author became a teacher after working as an engineer for 17 years. He has been in the field of education for 19 years now and is currently teaching math to classes 8, 9 and 10 at The Peepal Grove School, Chittoor, Andhra Pradesh. He can be reached at truthalonefrees@gmail.com.
