Meena Kharatmal and Nagarjuna G
Objective
Estimating the size of any small object or micro-organism is a challenging task for students and teachers. While observing organisms under the microscope, can we also estimate the size of the organisms? Should it be in centimeters or millimeters, or even more minute and tiny than these two units? There are units for observing smaller objects or micro-organisms that are too small to see with the naked eye. One of these units is called micron (μ) or micrometer (μm). We present a simple method to estimate small sizes and learn to use the micron as a unit of measurement.
How small is a micron? Why is it important to measure in microns?
Let us understand the scale of objects with the help of an image shown in Figure 1. The figures 1a and 1b show objects proportional to their sizes. The image in 1a begins by showing a known object, i.e., hair of 100 microns while the other objects are shown as gradually getting smaller and smaller in micron size. From particles that are visible to the naked eye, to dust particles, pollen, water droplets, fungus, spider web silk, smoke particles, bacteria and viruses. The image in 1b is an alternate representation to depict the smaller objects in reference to a known object (hair of 100 microns). The difference between bacteria and viruses is of 1000 times. When these objects are proportionally decreasing in micron size by a factor of 5-10, we cannot even show viruses in the diagram.
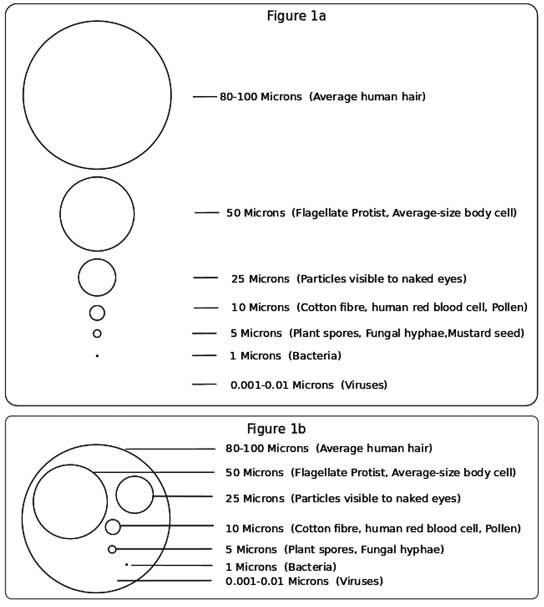
Anyone who can measure small sizes in millimeters can easily learn to estimate and measure objects in microns. Let us learn to estimate the size range of objects that measure in units of microns or micrometers, using a light microscope as well as a compound light microscope.
Links to curriculum
We surveyed all the middle school level science textbooks of classes 6, 7 and 8 (NCERT) to get an idea how the topic of measurement is connected in science topics and more specifically with biology topics. The textbooks do introduce and address the topic of measurement and specifically, micron as a unit has a brief mention.
We know that measurement is an activity that is already being dealt with in mathematics. In this survey, we noted that measurement was dealt mostly in topics relating to physics. These are measurements relating to distance, length, width, height, temperature, humidity, rainfall, wind speed, water absorption in soil, breathing rate, time, speed, amplitude, friction force, static force, earthquake, etc.
We also surveyed the two chapters (2 and 8) in the class 8 biology textbook related to micro-organisms, cell structure and functions on the assumption that these two chapters would address the concept of size and measurement, expecting the description of micro-organisms in microns or micrometer (see Figure 2).

To our surprise, we noticed that the entire chapter 2 which is about micro-organisms has no mention of measurement in micron. The size of micro-organisms is talked about as ‘small that cannot be seen with unaided eye’ (excerpt 1 in Figure 2). It is important to know how small is small! Students cannot get an idea of the scale of organisms that are less than 1mm in size, by a mere mention of ‘small’. The passage certainly does not address how such small sizes can be measured.
Chapter 8 which is about the cell structure and functions has a brief mention of the size of cells. Again, the size is mentioned as small. The unit of micron or micrometer is introduced as a millionth of a metre (excerpt 2 in Figure 2). The passage could at least have mentioned that 1 micron is 1/1000 of a millimeter and 1/1000000 of a meter. Secondly, the passage mentions the smallest cell size as 0.1 to 0.5 micrometer in bacteria, without explaining the dimension of the unit in relation to the known object.
Talking about measurement in a decontextualized area of mathematics and not connecting mathematical ideas in a context that demands it, is a serious disconnect we notice in our science education. This article attempts to provide the much needed connection.
The usual response
During our interventions with students (as well as teachers) ranging from middle, higher secondary, undergraduate levels, we frequently discuss the measuring of whatever they observed under the microscope. Upon asking what a micron is, we always received the response as, “10 raised to minus 6”, or 10 to the negative power of 6 (10-6)”. They stop at that phrase and then we cannot but ask “Of what?” Later some of them think a while and answer, “Of meter”. When asked to use their knowledge of conversion and estimate the size of a microbe, then all of them are in a fix, confused, and they make errors in conversion. It is to be noted that when students are thinking in terms of 10-6, i.e., in terms of a negative power of ten, they are at a loss when asked to convert this into microns. The difficulties could be due to the negative power/exponents (10-6), decimals (0.000001), fractions (1/1000000), etc., which are well-known hurdles in expanding mathematical imagination. The difficulty is, on the one hand, due to notation, and on the other, due to lack of introducing these concepts in terms of proportional reasoning.
While conducting the measurement activity with teachers, we use the light microscopes that are usually available in schools and colleges. Upon asking teachers to estimate the diameter of the visual field when observing from the eyepiece of the microscope, they respond it to be in centimeters (2 cm, 3 cm). However, when they are introduced to simple methods (see below) and then asked to estimate the diameter of the visual field, it comes as a surprise that it is about 1 mm or 1000 microns! It is important that teachers first estimate the visual field and then they estimate the size of the organisms under the microscope.
Measuring in microns
We start with some known units of measurements with simplified conversions for microns that are easy to understand or estimate the micron size (see Table). We can estimate or measure the objects under a microscope in microns by using simple methods and minimal materials with simplified calculations and conversion from known units of measurements.
| Units | Conversions | Objects |
|---|---|---|
| 1 meter (m) | 100 centimeters (cm) | 1 meter scale |
| 1 centimeter (cm) | 10 millimeters (mm) | Average width of index fingernail, pumpkin seeds |
| 0.1 centimeter (cm) | 1 millimeter (mm) | Grain of sand, mustard seed |
| 1 millimeter (mm) | 1000 micrometers (μm) or microns (μ) | Diameter of a pinhead, frog eggs, flea |
Table: Known units of measurements and their conversions.
Let us begin with imagining the space of 1 mm that can be observed with our naked eye. For example, 1 mm is the space between two divisions on the centimeter side on a ruler. This space of 1mm is equal to 1000 microns. As in the initial stage, it may be difficult to imagine a space of 1 micron, we can develop the practice of imagining the space of 1000 microns. Figure 3 shows the observation of the visual field of a compound light microscope depicting the space of 1mm as equivalent to 1000 microns between two divisions. The total magnification of this visual field is 100X (10X eyepiece and 10X objective).
We demonstrate it by using two simple methods as shown in Figure 3. The first image is taken by placing a transparent ruler under the compound light microscope. The second image is taken by placing a transparent graph under the compound light microscope. Note that we have taken all these images of real observations using a smart phone by placing it carefully on the center of the eyepiece of the microscope.
- The ruler method: We know that a ruler has two units of measurements – inches and centimeters. We can place the transparent ruler under the microscope to see the divisions of the centimeters. We know that two divisions within the 1 cm scale is 0.1 cm which is equal to 1 mm. We also know that 1 mm is equal to 1000 microns. We can observe this space of 1 mm i.e., 1000 microns under the microscope to get an estimate for measurement to learn how much of the visual field is 1000 microns.
- The graph method: On a graph paper, each grid is of 1 sq cm with 10 equal divisions. Each square inside the grid is 1mm (1 sq mm). We know that 1mm is 1000 microns. A transparent graph paper can be made by photocopying a graph page on a butter paper. We can also use a readily available grid image and print using a laser printer. A small grid of 1 sq.cm can be cut and placed on the slide to observe the divisions.

Image 1 is taken by placing a transparent ruler under the microscope. While image 2 is taken by placing the transparent graph paper under the microscope.
It is important to note that in the light microscopes usually found in school and college labs, we have observed the visual field to be of 1000 microns with the ruler method. Figure 4 shows the variation in the diameter of the visual field observed. In Figure 4, image 1 of the light microscope shows the visual field space of 1mm i.e., 1000 microns, whereas image 2 of the compound light microscope shows the visual field space of 2mm (2000 microns). Therefore, it is necessary that the visual field of the microscope used in the study be first calibrated for the space.

So, certainly we can see a space of 1000 microns (in a high resolution kind of compound light microscope, we can actually see a space of 2000 microns) with our naked eye! Performing observations with these two methods will provide us with an estimate of a space of 1000 microns in the visual field of the microscope. The diameter of the visual field is what we need to measure to develop proportionality, which is what eventually helps us to do the estimation.
Now that we know about the scale of 1000 microns in this space, we can use it to estimate and even measure any object that is placed within these two divisions.
Estimating small objects in microns
Let us do a simple activity of estimating and measuring a very small object, for example, a single hair strand (or fibre strand) using one of these methods.
- Estimating the size of a single hair strand: Let us first begin by guessing the size of a single hair strand (or a single fibre strand) in microns. It can be noted down and verified after the activity. We demonstrate it using the graph method (see Figure 5) by taking photographs of the hair strand under the compound light microscope. It involves direct observation, taking photographs, using drawing work, followed by extrapolation to estimate the size in microns.
a. The grid of the transparent graph seen as the visual field under the microscope.
b. Placing a hair strand on a slide and covering with the transparent grid to observe under the microscope.
c. This image was used to create an outline of a thick line (or a rectangle) overlapping the image of the hair strand.
d. Now that we have a line of known size, we can make copies that can occupy the space of 1mm. In this image, there are 15 such lines that are occupying the 1 mm space i.e., 1000 microns. - Estimating small size organisms: Let this be an activity. We can do this activity by observing soil samples under the microscope. However, for practice we provide images of micro-organisms taken under the compound light microscope. These images have a total visual field of about 2000 microns. Even while observing organisms under the microscope one can apply this method to estimate their size in microns.

1. The visual field showing the grid of 1000 micron.
2. A single hair strand within the 1000 micron grid.
3. A rectangle is created overlapping the single hair strand.
4. Each rectangle is then arranged side by side to fill the 1000 micron grid.
Now that we know, there are 15 hair strands that occupy 1000 microns, we can estimate the size of a single hair strand by using a simplified calculation and conversion method as shown in Figure 6. So we get an estimate of a single hair strand to be of about 67 microns. We can check whether our guess is correct. Of course, this would also depend on the thickness of hair which varies from person to person. Teachers can motivate the students to find out whose hair is thickest in the class, and who has the thinnest hair? Students and teachers can collect quite a lot of data from the population of the school, and it can be a lesson in statistics as well!
Now we can apply this simple method and simplified calculation to estimate the size of micro-organisms under the microscope. Let’s do this as an exercise!

Task 1. Estimating and measuring the Hydra: Observe Figure 7 depicting a Hydra with an additional bud (total magnification is 100X). For ease of estimation, we have overlaid the total diameter of the visual field that is about 2000 microns (1st image). Given this space of 2000 microns, we can estimate the length of the whole Hydra with the tentacles. Observe the 2nd image and estimate the length. You can write your measurement on the image itself.

Task 2. Estimating the thickness of a paper: We can estimate the thickness of paper by applying proportional reasoning. We know that a book comprises of several hundreds of pages. Let’s understand how to estimate the thickness of a page.
- Take a small bunch of pages so that the thickness of the bunch is about 1 cm (i.e. 10 mm or 10000 microns).
- Note the page numbers that have been occupied in this 1cm thick bunch. For example, 176.
- Since the page numbering is done on both the sides and we want to estimate for a single paper, we can divide this number by 2. For example, 88.
- Now we know that 88 papers are occupied in 10000 micron space (1 cm), then 1 page is about 114 microns.
Likewise, we can estimate the size of smaller objects that are in micron units. For example, by using the above method, we can estimate even the thickness of a cover slip in microns!
Summary
We presented a simple method to estimate the size of small objects in micron size. We can use our day-to-day objects and develop a method of estimation using a light microscope, transparent ruler and graph paper. By applying simple conversions and proportional thinking, we can realize the size of objects in microns.
To do tasks – write to us
Can you think of any such examples where we can estimate the size of smaller objects? Develop such tasks and by using the above method calculate and estimate the size. You can send us your examples by email or post.
Find out if there are any other units that are used for even smaller objects than micron size. Can we apply this method of conversion from known units to estimate the size of objects in nanometers? Write to us with examples at – cube@hbcse.tif.res.in.
Acknowledgements
We acknowledge the CUBE lab members M C Arunan, Mayur Gaikwad, Aashutosh Mule, Jaikishan Advani, Kiran Yadav, along with students and teachers.
We acknowledge the support of the Government of India, Department of Atomic Energy, under Project No. 12-R&D-TFR-6.04-0600.
The authors are with the Homi Bhabha Centre for Science Education, Tata Institute of Fundamental Research. They are involved in developing teaching and learning modules at school and college levels. They can be reached at meena@hbcse.tifr.res.in, nagarjuna@hbcse.tifr.res.in.
