Saroja Sundararajan
Usually, it is a small percentage of students who really look forward to a maths class. For the rest, it spells gloom. Why? What should we do to help rid our students of their math phobia?
Imagine a plain brown cake placed on a table. Next to it is another cake with colourful toppings, laced with mouth-watering icing and beautiful decoration. Which do you think a child will choose? Almost certainly, the second one. Why? Because the presentation is very attractive.
In junior classes when you are teaching, say ‘subtraction’, you can make it attractive for your students. Draw a basket full of apples on the board and ask your students to think of reasons why apples are disappearing from the basket. As your students give their reasons, they cross out one apple in the basket.
Your students can be creative and funny with their reasons. Here are some of the reasons I have been given by my students:
“A teeny-wheeny mouse came and stole one apple at night.”
“An alien from Jupiter gobbled up one apple.”
As your students give their reasons, write 10 apples – 1 apple = 9 apples.
9 apples – 1 apple = 8 apples and so on.
Such exercises will not only help evince an interest in the subject for the students, but will also enhance their creativity. Permanent learning takes place when you integrate art with mathematics!
In this article I will show you how you can include both the visual arts (drawing, colouring, cutting, etc.) and the performing arts (dance, music, storytelling, etc.) in your math classes.
Let us see examples of each and what effect they have on the learning skills of the student.
Visual arts
a. Intuitively learn a higher level concept.
Task 1: (class 6 – number patterns)
Draw a kolam (rangoli pattern) between the two existing kolams by decoding the pattern.
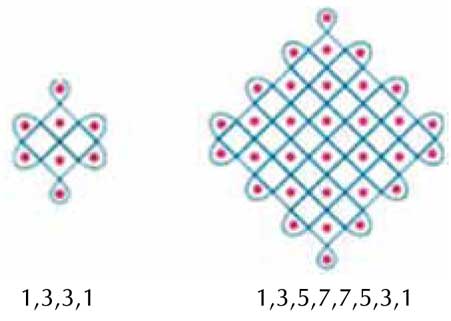
Mathematics combined with art not only brings out the number sense but also creativity in the student. A student going to higher classes learns that the sum of the first n consecutive odd integers will yield a square number ‘n2’. How can we lead the students to grasp this concept intuitively in the lower classes? Look at the odd integers placed in rows, together they form a beautiful square each. Look at each of them sideways!
b. Promote lateral thinking (classes 7, 8 – congruency)
Task 2:
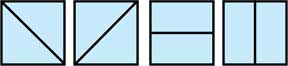
- Fold and cut out the BIGGEST SQUARE from a rectangular sheet of paper.
- Draw different lines inside the square to show that the lines divide the square into two halves.
- Ask your students to think out of the box, think of solutions other than these obvious ones.
c. Encourage perspectives: (class 8 – three dimensional solids)
Task 3:
Ask students to draw a square as above. Tell them that they should turn this figure into a 3D figure. It should look as though we are entering a room through a long corridor. How will you modify the original square to get such an illusion?
This is what perspective art is all about.
Perspective is an art technique for creating an illusion of three-dimensions (depth and space) on a two-dimensional (flat) surface. Perspective is what makes a painting seem to have form, distance, and look “real.”
The mind is cheated into seeing something that does not exist. It requires skill to produce such art.
d. Correlate numbers with nature: (class 8 – real numbers)
Fibonacci was an Italian mathematician from the Republic of Pisa, considered to be “the most talented Western mathematician of the Middle Ages”.
He discovered a number series known as the Fibonacci series.
1,1,2,3,5,8,13,21,34………….
The sum of any two consecutive numbers in the above series, gives the next number in the series: 1+1 = 2; 1+2 = 3; 2+3 = 5; 3+5 = 8 and so on.
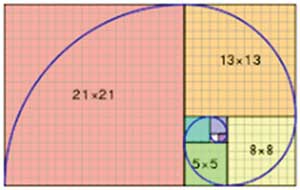Task 4:
When each of the numbers is depicted by a square, drawn adjacent to the previous one and a curve is drawn as given here, it would form the Fibonacci spiral. This spiral is found abundantly in nature.
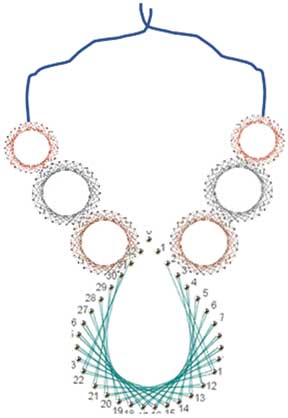
e. Design jewellery by creating curves with straight lines: (class 8 – circles)
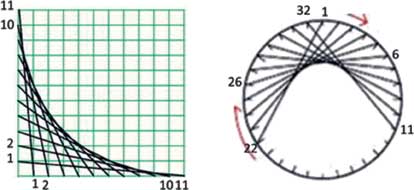
A seemingly impossible task made possible by juggling numbers.
Experimenting by joining numbers differently will produce different designs.
Task 5: Using these ideas, create jewellery designs.
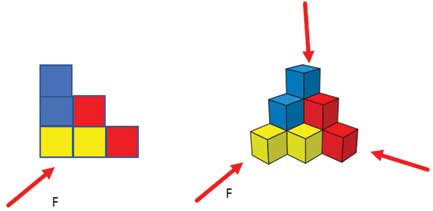
f. Enhance the skill of recognizing and sifting which will help in building architectural skills: (class 8 – 3D shapes)
In perspective drawing, students learn to convert a 2D visual into a 3D visual. Here, conversely, they will learn to represent a 3D figure in its 2D form. This skill comes in handy when students are working as architects and have to draw an elevation or a plan of a building. The elevation is the front or side view which is the vertical visualization of an object. The top view is the horizontal view of the object.
Task 6:
Twelve 2D forms of the central figure is given here. The centre piece is the 3D form.
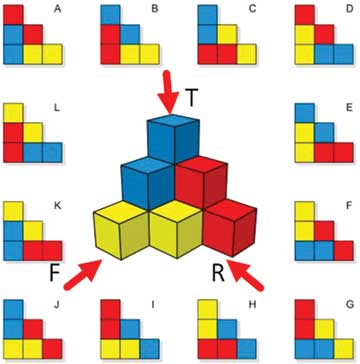
Is it possible that you can identify the correct 2D form which matches the central 3D figure?.
Performing arts
1. Music: Music and mathematics go hand in hand. Music is based on mathematics in its metre, rhythm, pitch, tone, etc.
Pythagoras, the famous mathematician, said that the string of an instrument determines its pitch. In the primary classes teaching mathematics through song and dance is the best form of teaching.
https://www.youtube.com/watch?v=lqw2iAv3Yb4
https://www.youtube.com/watch?v=ZzeDWFhYv3E
https://www.songsforteaching.com/math/multiplication/multiplyingmagic.php
These websites will give the teacher ideas as to how music can be used in the math classroom.
2. Storytelling:
a. Spatial skills and fractions through narration (std 6, 7, 8 – geometrical shapes)
Tangram is an ancient Chinese puzzle. A square figure is divided into seven pieces as follows:
1) 2 big triangles
2) 1 medium sized triangle
3) 2 small tringles
4) 1 square
5) 1 parallelogram
The Chinese used to spend their free time making meaningful figures with all seven pieces assembled together.
Here is the tangram.
Photocopy this square and keep at least 10 copies of it.
Each copy of the square should be neatly cut into the seven geometrical pieces and placed in separate envelopes.
Given below are several figures made using the tangram pieces.
Note that all the seven pieces are used in each figure.
Make up a story using these figures.
According to the sequence of your story, on a chart paper, assemble and paste the figures.
Read out your story to the class.
Here are the figures that you will use for your story:
Storytelling helps in
• Bringing out creativity in the student.
• Developing the art of narrative skills.
• Shedding inhibitions and
• Developing spatial skills in mathematics while cutting, assembling and pasting the pieces.
Surely by now you can appreciate the immense value of integrating art into the mathematics curriculum. But remember these activities have to be woven into regular classroom teaching rather than be given as extra project work, only then will the objective be achieved.
A sample lesson plan integrating art with mathematics
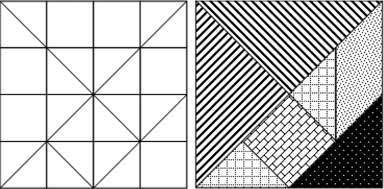
• On a graph sheet of paper, draw the tangram square.
• Make multiple copies.
• Cut them out, colour or shade each piece differently and keep them ready for the activity (as shown in the black and white image on the previous page).
If the whole square is 1 unit square, calculate the area of each piece as a fraction of the whole. For example, each big triangle = 1/4 of the whole.
Similarly calculate for each piece.
Learning objectives:
At the end of the lesson, the student will be able to:
• Draw a tangram square, dividing it into the seven geometrical shapes.
• Colour each piece aesthetically.
• Cut out each piece accurately.
• Calculate the fraction that each represents of the whole and write the fraction on each piece.
• Choose and assemble the pieces in such a manner that the total of the fractions equals the fraction asked to be formed.
• Add fractions with ease.
Materials required: A graph sheet, pencil, ruler, colour pencils, a pair of scissors, glue.
Lesson task:
Make multiple copies of the pieces.
Task 1:
• Choose the appropriate shapes that you require so that they add up to the fraction asked for.
• Assemble them to make a meaningful figure.
• In your notebook, either paste them or copy and draw the shape.
• Repeat the task for each of the following fractions.
a) 1/4 b) 1/2 c) 3/4 d) 1/8 e) 5/8 f) 1
An example has been given for you.
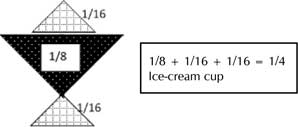
Task 2:
To the above figure, add one more piece and make a different shape so that the total fraction of the new shape is 1/2.
Think…
1. Were you able to complete the tasks with ease?
2. Which part of the activity did you find difficult? Why?
3. Can you make your own activities using tangrams?
(This lesson plan can be used when students are taught fractions, geometrical shapes or polygons.)
Solutions
Task 1:
Task 2:
These are also halves of each whole.
Task 3:
Task 5:
Task 6:
The author, who was the first CBSE teacher to get the Best Teachers National Award in 1986, has had a very successful teaching and teacher training career spanning over five decades. She was the Director of the Teachers’ Centre at Springdales School, New Delhi and is the author of several textbooks. She now works on a freelance basis from Chennai. She can be reached at saroja.tvs@gmail.com.