Monica Kochar
Continuing our series for senior school, this article explores a different way of dealing with sets. Usually one starts with information, symbols and then goes to applications. But can this sequence be turned around? Can we start the topic without using the word ‘Sets’? Rather can we come to the word through reasoning and hence show a perspective for the existence of the concept of Sets?
Are you as a teacher adventurous enough to take a risk?
Try these suggestions below and let me know how they worked for you.
Beginning
Let us start with a real life situation. Give students the following problem and ask them to solve it in any way they wish to. To ensure that no one is left behind, let the task be in groups of three. Each group ought to have at least one student who is good at math.
Problem
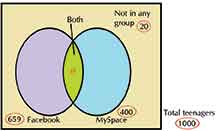
The teenage fascination for Facebook has suffered a dent with some teenagers above 14 moving to the newer MySpace. Some teenagers are also moving away from social networking altogether. In a random survey of 1000 students in a neighbourhood, it was found that 659 used Facebook, 400 used MySpace and 20 did not use either.
a. How many are loyal to both?
b. How many are still totally loyal to Facebook?
c. How many are loyal to Myspace?
Students will come up with different methods. Let them come to the board and show the different methods. Allow them to use numerics or pictures to demonstrate.
(This process is very important for this is where students will see that there are many ways of solving a problem. The brain learns to be flexible and creative. Students will also learn to pick their personal favourite method.)
Mathematics is all about finding efficient ways of solving a problem. Efficient would be a method that is short, crisp, and valid for all types of problems. Using this as a perspective, introduce the picture method for them.
(Note – till here, there is no mention of sets or venn diagram.)
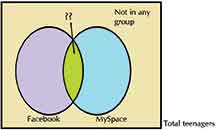
Let us try and solve this visually.
The rectangle represents the total number of social network site users. The circles represent the individual groups.
Q – What does the green space represent?
Q – Which colour(s) shows users of Facebook only?
Q – What does yellow represent?
Ask students to write down all the numbers in the diagram from the problem
But wait! 659, 400 and 20 add up to more than a 1000!
That is because the green portion is common to both Facebook and Myspace and is added twice!
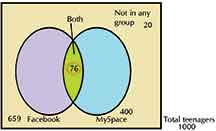
Hence green portion = 659+400+20–1000=76
So, people who like:
a. Both = 76
b. Facebook only = 659-76 = 583
c. Myspace only = 400-76=324
(Even now, do not talk of venn diagram or sets!)
Ask students to solve another problem using this method.
A survey was conducted to check the popularity of two newspapers. Out of the 100 people interviewed, 35 like Times of India, 22 Hindustan Times, 20 like both and the rest do not read either of the newspapers. How many do not read either?
NOW bring in the vocabulary!
Inform them that John Venn thought of this way of solving problems. Hence it is called the venn diagram. Inform them that this is a graphic organizer and can be used in different situations as shown:
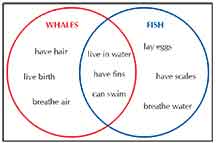
Comparing whales and fish
(source: http://www.learnnc.org/lp/pages/2646)
Explain/recap sets, universal set, intersection, union, venn diagram and any other concept that you wish to teach/recap. This is where the textbook steps in. What I would suggest is to keep one lesson for building perspective using the two problems I have shared. Keep some lessons for textbook work.
And then finally one lesson for a stretcher…
S T R E T C H yourself!
All my life both as a teacher and student I have seen textbooks solve sets problem using only 3 sets venn diagrams. But why are we limiting ourselves to just the three sets? Can sets come only in threes?
John Venn said venn diagrams can be used for any number of sets. But it gets increasingly complex!
Try!
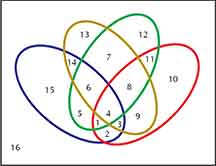
Construct a venn diagram for the following 4 sets:
A={1,2,3,4,6,7,12,15}
B={14,12,11,7,5,6,8,1}
C={13,11,10,5,6,7,4}
D={9,10,5,6,1,2,3,8}
U={all of above and 22}
(Hint: You will get 16 regions as shown below)
Go to weblink: http://www.math.csusb.edu/notes/sets/node5.html to see more of >3 sets venn diagrams.
The author has taught math for 19 years in Indian and international schools. All through her teaching career she was known as a very creative math teacher who helped students get over their math phobia. Currently she works with teachers to kindle the same fire through her sessions in math, exploring the self and CCE. She also works as a curriculum developer and mentor for math curriculum. She can be contacted at reachmonica@gmail.com. She also has a facebook page www.facebook.com/humanemath.