Athmaraman R
The need
To succeed in mathematics, students need competency in its content, concepts and skills. Teaching should aim to provide all three. Regrettably, the traditional objectives-based approach to teaching has not yielded the desired results. In particular, conceptual understanding is often feeble and even nonexistent among learners. For instance, many children solve multi-digit subtraction problems using the procedure of “borrow and regroup” without knowing why they do so. That the ‘product of two negatives makes a positive’ is an interesting result but there is little inclination among students to know why it works so. For them, to secure marks, ‘how’ of the procedure is more essential than ‘why’ of the process.
Concepts are a way to organize and make sense of learning and when they are not assimilated properly, the whole exercise of teaching and learning becomes worthless.
The belief that ‘one of the most tragic shortcomings in our system of mathematics teaching is the students’ lack of conceptual understanding’ conceals the unpleasant fact that such a deficiency exists to some extent even among the teaching community. A mathematics teacher, who is to retire from service shortly, sent an urgent request to a consultant: “Sir, I need exact answer for the following question, which I have to discuss with my class tomorrow. They have brought this question:
Name the smallest single digit number:
A) -9 B) -1 C) 0 D) 1”
In the first place, the question is vague since it does not indicate whether it refers to a natural number or a whole number and naturally leads to uncertainty in comprehending a concept. When the same question was posed to another teacher, she responded correctly declaring that 1 is the answer if we consider the natural number system. However, she struggled a lot when she was asked to consider the question with regard to other systems, for instance, the system of complex numbers. This shows the absence of confidence stemming from the lack of awareness of the ‘order relation’ concept.
There is an obvious striking correlation between teachers’ mastery of concepts and student achievement. Failure to grab fundamental notions leads to poor performances resulting in dejection and fear of the subject. Primary math concepts intrinsically hook up to each other, because of which the learner who comprehends one concept will figure out a consequent one easily and swiftly. If a learner is not thorough with the notion of ‘a multiple of a number’, how will he/she handle the idea of ‘least common multiple’?
Concept mastery being the essential foundation for doing well in mathematics, the question arises as to what strategies a teacher should adopt to help the learners gain conceptual understanding. We try to list a few techniques here.
Examples and non-examples
Euclidean geometry in schools is based on three essential undefined terms: a point, a line and a plane. (‘Space’ may be reserved for higher levels). One cannot define them but can quite possibly describe them. For example, a dot is used to represent a point. (A dot has a little breadth and height and so is not a point by itself but only a representation!). A point tells where something precisely is and begins to build geometry.
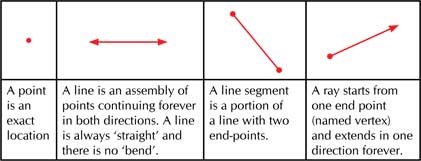
One can now define an angle. An angle is a pair of rays (called sides) with a common end point (called vertex). An angle is a very important concept, which is often not understood entirely.
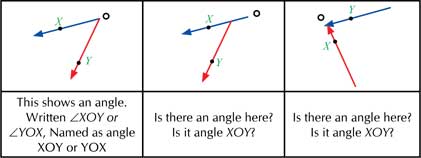
To strengthen the concept further, discussion on questions of the type that follow may help the teacher:
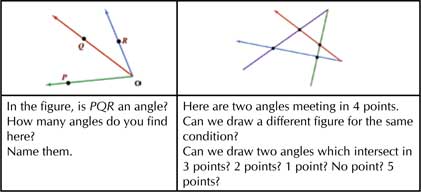
Exploring different possibilities, thus leading to a lot of communication between the teacher and the taught, will establish clarity in thinking.
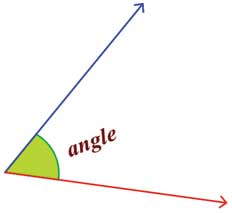
Quite often, one finds figures like the ones given here:
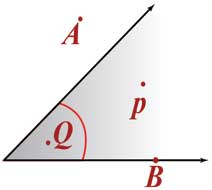
This figure may lead to an erroneous idea that the green-coloured area is the angle, whereas in reality, the angle is simply the couple of rays and has nothing to do with the green-coloured zone. What if a student draws a larger green zone for the same angle? Will it be a different angle? If the angle is viewed through a magnifying glass, the shaded area will seem bigger and what will it mean then? One may feel that this is a silly difference to point out, but we will see how it is important.
In the figure shown here, which are the points that belong to the angle? Only B is the eligible candidate. Just carefully go through the definition of an angle above. P and Q are in the interior of the angle while A is in its exterior. The learner has to be given plenty of illustrations as examples and non-examples.
[To digress:
- An angle may also be defined as the amount of ‘turn’ between two rays around their common starting point; in this case the concepts have to be listed and approached appropriately in a different way.
- Here we have not dealt with the very important difference between an angle and the measure of an angle. The practice of marking with an arc the interior of an angle perhaps is due to the mix-up between these two concepts].
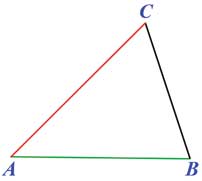
How do you define a triangle? It is a closed figure consisting of three line segments linked end-to-end. While giving such a definition, the teacher should keep in mind that it is linked to another concept, “closed figure”. It also assumes that the three points where the line segments meet are not “collinear” (which is one more concept, left usually to the intuition of the learners). Because of this difficulty, a strict definition would be as follows:
Given three points A, B and C (called vertices) that do not belong to the same line, the union of segments (called sides) is called a triangle (denoted by ∆ABC). Note that the sides can be seen as parts of rays and so ∠BAC, ∠ABC, and ∠ACB are the angles of the triangle.
A point lies in the interior of a triangle if it lies in the interior of each of the angles of the triangle. A point lies in the exterior of a triangle if it lies in the plane of the triangle but does not lie on the triangle or in the interior.
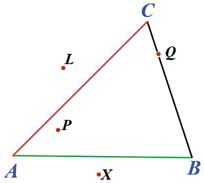
In the figure, does P belong to the triangle? No, it is in its interior. How about Q? Surely it belongs to the triangle since it lies on the segment connecting B and C. The points X and L are in the exterior of the triangle.
The teacher should be able to create adequate non-examples and examples.
Study the following situation

The teacher has explained the theorem about the angle in a semicircle.
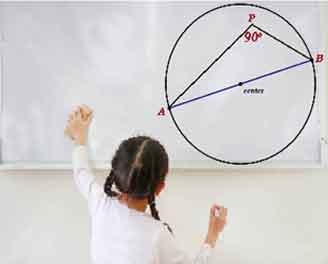
The student draws a figure and asks if it is correct since P is “in” the semicircle.
This confusion is due to the misconception that the interior also is part of the circle. The circle, by definition, is made up of the curve only. The point P has to be a point of the curve for the theorem to be true.
Many such examples can be given where such false impressions arise, pointing to the need to use illustrations and counter-illustrations to make things unambiguous. This will help to gain a precise and accurate understanding of the concept. Learners need to be told how our ‘loose’ (viz, non-rigorous) communications actually mean precise articulations.
For example
| Imprecise statement | Precise statement |
|---|---|
| The sum of the three angles of a triangle is 180° | The sum of the measures of the angles of a triangle is 180° |
| The perimeter of a square is the sum of its sides. | The perimeter of a square is the sum of the lengths of its sides. |
While aiming at precise conceptual understanding in teaching, teachers should be able to give a number of precise and imprecise definitions in contrast.
Visualization
Visualization in mathematical learning can achieve a lot. It entails setting up a link between information about concepts, which are previously unknown, and understanding, which gradually develops. It leads to the creation of mental images of given concepts. At the beginning stage, visualizing a fraction as a part of a whole is a familiar example. It is the experience of Singapore mathematics that the sequence “abstract ⇒ visual model ⇒ symbol” influences learners to do problems in their heads, to articulate them out and to draw visual images of the problem before using the concepts and language of mathematics. In fact, algebraic ideas are disseminated in a concealed manner. Visual justification of concepts involved is the preliminary outcome, which can be strengthened by rigorous supplements subsequently. While one need not and cannot depend on this technique always, the capacity to visualize can often simplify the process. Encouraging the learner to visualize will be quite rewarding. Diversity in approaches can sometimes be an added bonus.
Observe how two learners may approach the problem of finding the area of a given right triangle:
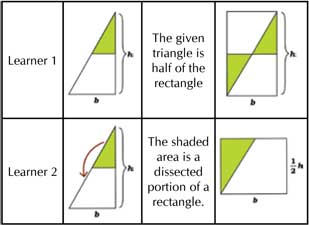
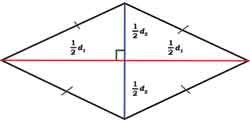
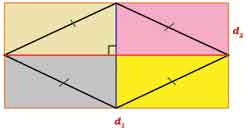
Similarly, while computing the area of a rhombus, one may visualize it as a union of four isosceles right triangles or as half of a rectangle passing through its vertices.
Or
Visual reasoning is not restricted to geometry or spatially represented mathematics. Here follows an example based on the concept of proportions.
A boy of height 2 metres stands at a certain distance from a lamp post of height 6 metres and casts a shadow of 4 metres on the level ground. Find the distance between the boy and the lamp post.
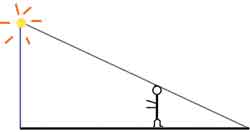
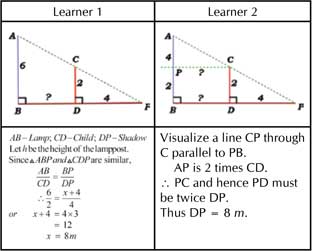
For learner 2, visualization shortens the calculations, since clarity of concept of proportions seems to influence him via his mental images.
Let us consider one more example, now from arithmetic.
Mr Bumble withdrew some money from a bank. He used half the amount to buy things from a supermarket. He spent one-third of the remaining sum towards the purchase of some books. Lastly, he spent one-fourth of the sum left over to pay mobile phone charges. Now he had a balance of Rs.900 with him. How much did he withdraw from the bank?
Learner 1:

Learner 2:

Learner 3:
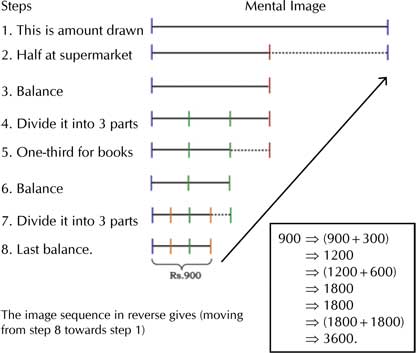
The first two learners follow the traditional approach whereas the 3rd learner has conceptualized the happenings with the help of a visualized mental image, which has given an elegant way of solving the problem.
We note that the process of visualization could be through pictorial images or schematic representation. It is crucial that the teacher makes this clear to the learners. An experienced teacher will also find that most students gifted in mathematics are non-vizualizers.
It is perilous to always take visual justifications as ‘proofs’; visual thinking in mathematics fell into disrepute since it can often be deceptive’ (a justification of this statement is beyond the scope of this article). Nevertheless, after computer science began to boom, visual thinking rehabilitated the epistemology of mathematics.
Probing questioning
To promote inquiry into and perception of various aspects of concepts, Socratic dialogue between learners and the teacher is crucial, based on asking and answering a series of interlocked, sequential questions, to stimulate critical thinking and to draw out ideas. Asking questions at the end of a lesson as a ritual does not serve the purpose of questioning. Very few teachers are aware of the distinction between formative evaluation and summative evaluation and hence do not provide for punctuating teaching with questions that constitute formative evaluation – that is, checking whether the learner has mastered every concept before the teacher goes to the next concept/point.
Questioning should be utilized to clarify notions, challenge assumptions, examine reasons and perspectives and to explore implications and outcomes of proposals and statements made during discussion. Frequently, the responses may be inappropriate-off at a tangent, invalid and meaningless, but the learner should be allowed to make mistakes. The best way to learn concepts is to learn how the ‘trial and error’ mode of learning will make for a stronger grasp of concepts.
Here are some samples that direct towards clarification of concepts:
1) Does ‘zero’ mean ‘nothing’?
(If there is zero degree temperature on a hill station, does it mean there is no temperature?
Write the numeral ‘twenty three’. You get 23. What is between 2 and 3 here? Nothing! Then why don’t you put the numeral for ‘zero’ there?)
2) It is said 0.9999…. is equal to 1. When you have endless number of 9s following one after another, how is this possible?
Method 1 Method 2 Method 3
3) What is the value of the product 05x0-5?
(0-5= 1/05 is undefined)
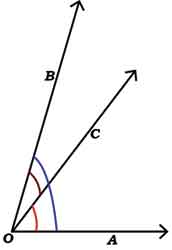
4) Comment: “Adjacent angles are two angles that have a common vertex and a common side.”
(Study the figure shown here. ∠AOC and ∠BOC are adjacent angles. Are ∠AOC and ∠AOB adjacent? No doubt, they have a common vertex and a common side. Adjacent angles should not have common interior points!)
5) Comment: “The slope of a line is zero. Therefore it has no slope.”
(A horizontal line has a slope equal to zero; a vertical line will have no slope, and “the slope is undefined”.)
6) Comment: “If the measures of the corresponding angles of two polygons are equal, their sides will be proportional.”
(No. Try to draw two rectangles whose sides are not proportional.)
7) AC is one way of naming the line shown here. In how many more ways
![]()
can it be named?
(11 more ways.)
8) Why cannot 48 be the LCM of 18 and 24?
(48 is not a multiple of 18; 18 does not divide 48 evenly.)
9) One side of a right triangle is 5 cm. Find the lengths of the other two sides.
(The students may be tempted to give the answer as 3 cm and 4 cm, thinking that only the hypotenuse will have length 5 cm. There are many answers!)
The last two questions belong to the category of open-ended questions. These are quite useful to initiate a forceful debate of the concept discussed.
Investigations and project work involving collaborative learning are some of the other avenues available to promote conceptual mastery.
(Open-ended questioning, investigations and project work are themselves topics deserving separate discussion and are not a part of this article).
Conclusion
To enable concept-mastery, teachers need to encourage divergent and reflective thinking. Coupled with appropriate questions, interactive sessions would promote confidence and participation that induce healthy competition.
Contributions made by students make it an enjoyable experience for them. Enabling visualization, providing illustrations and counter-examples and facilitating a communicative environment in the classroom are some ways to achieve concept mastery.
The author started his career in 1962 and has worked as a teacher, headmaster, researcher, academic advisor and math educational consultant. He has served as the Secretary of The Association of Math Teachers of India (AMTI) and also as the editor of the journal Junior Mathematician. He has authored several books and written textbooks for NCERT and Tamil Nadu State Board. He can be reached at athmaramanr@gmail.com.
