S N Gananath
The definition of a good mathematical problem is the mathematics it generates rather than the problem itself. – Andrew Wiles (English mathematician)
Long ago, there lived a family in a village and the father was on his death bed. He called his three sons and asked them to divide the horses he owned among themselves after his death. The eldest son gets 1/2 of them, the youngest son gets 1/9 and the one in between gets 1/3.
But this created a problem as there were 17 horses and naturally his children were confused. How do we divide 17 horses as per his wish without cutting them?
This is a folk mathematics problem and it is no surprise that this popular puzzle is prevalent in many parts of India and I have discovered it in Rajasthan, Bihar, Andhra Pradesh, etc., in my interactions with schoolteachers and even children. A closer examination reveals the enormous potential to convert such problems into a series of pedagogically sound and motivating activity sets. Some of the core objectives of mathematics teaching, viz., problem solving, creating extensions, problem posing, generalization, computational automaticity, spatial thinking and so on can be addressed by an imaginative and zealous teacher. This article intends to explore such a possibility and create appropriate pointers.
Let us consider another puzzle.
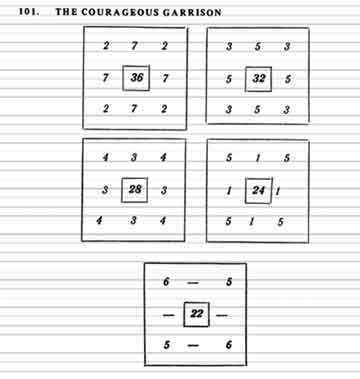
The courageous garrison
This appeared in the outstanding puzzle book Moscow puzzles by Boris A. Kordemsky, a book that has inspired a generation of mathematics enthusiasts.

The solutions are here. You will notice the rearrangement of these boys after each assault.
Curiously, a puzzle very similar to this is popular in different parts of India. In that puzzle, a king has 32 horses and has arranged them in a square like this (see Fig 2) such that he can see 12 horses along each line of sight as indicated in the picture.
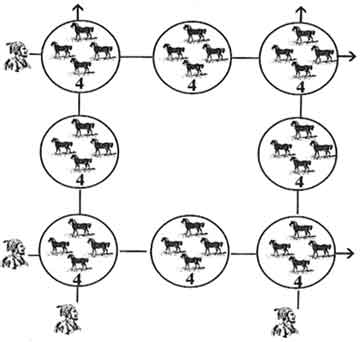
The king has instructed the watchman to make sure there are 32 horses all the time, no more no less. Every circle must have at least one horse. He thinks he is smart and so has devised a shortcut to verify this. Regardless of the number of horses in each circle, he just checks the total number of horses along each line of sight.
A traveller comes in the evening and meets the watchman. He has four identical horses and wants to tie them along with these 32 horses. The watchman refuses initially but agrees later when an incentive is offered. The traveller is asked to tie the horses conforming to the ‘12 in a line’ rule. Here is the arrangement. Total = 36 horses.
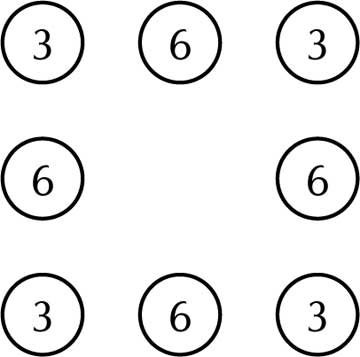
The story continues. In the middle of the night, the traveller escapes taking his four horses. He also steals four horses. Now only 28 horses are left and the watchman has to arrange them hurriedly, before the king comes and he succeeds! How does he do it? Can you try?
I always thought this a great opportunity to understand the pattern and explore a number of mathematical concepts.
1. Can we solve the problem if the number of horses is other than 32, 36 and 28?
2. Is there a general rule in placing the horses
a. in the four corners do you place >4 or <4?
b. Is it possible to solve this problem if the number of horses is odd? How?
c. What is the theoretical min and max?
d. Does it work if the shape is a triangle instead of a square?
3. Is this a low floor, high ceiling kind of activity? How?
We shall discuss these later.
But for now, let us revisit the earlier problem of sharing 17 horses among three children. According to the story, a wise man was passing by and volunteered to help. He had one horse with him which he gave them, thus making it 18 horses. He computed 1/2 of 18 (nine), 1/3 of 18 (six) and 1/9 of 18 (two) and added them, i.e., 9+6+2=17. He took back his horse and proceeded to the next village. The solution may not sound ‘mathematically convincing’ but everyone said, “Wah, such a smart idea!”
Can we find any pattern and get solutions if the number of horses and the shares of the three children are different? When I challenged the teachers regarding this interesting variation, the response was truly disappointing. They did not see this as an opportunity to explore the world of puzzles and mathematics. This is sad. In the classroom, we cannot afford to miss ANY opportunity to promote mathematical learning. This is especially true here as the background story is both interesting and motivating.
To illustrate this point, let us explore further with different assumptions. (Reminder: Add the extra horse that belongs to the traveller before computing)
Case 1: Two children; they get 1/2 and 1/3. How many horses?
Answer – 5 horses
Case 2: Three children; they get 1/2, 1/3 and 1/8. How many horses?
Answer – 23 horses
Case 3: Three children; they get 1/2, 1/3 and 1/7. How many horses?
Answer – 41 horses
Case 4: Three children; they get 1/2, 1/3 and 1/6. How many horses?
(Hint: Convert this problem into a linear equation)
Case 5: Three children; they get 1/2, 1/4 and 1/8. How many horses?
Case 6: Four children; they get 1/2, 1/4, 1/8 and 1/16. How many horses?
Case 7: Five children; they get 1/2, 1/4, 1/8, 1/16 and 1/32. How many horses?
Did you arrive at a pattern after solving cases 5, 6 and 7? What pattern?
Let us now revisit the King’s horse puzzle. Here are some random solutions.

Can you notice any pattern/s here? Can you create more problems similar to this? Is there a possible use of this in real life?
This is a case of number partition, but of a minor-league; not as serious and profound as what professional mathematicians study. Nevertheless, for a school child this is no mean path of joyous discovery. In the hands of persevering and competent children, this can even result in an independent mathematical creation.
Moving on, let us consider this folk puzzle.
There are 100 rotis to be distributed to 100 people. Easy, but there is a catch. This group has some men, some women and some children. Men get 10 rotis each, women get 3 each and children get 1/2 each. The question is how many men, women and children are there?
There are infinite variations of this Diophantine equation1 that has emerged in almost all parts of the globe and not unsurprisingly, this puzzle is a perennial source of excitement for teachers, children and even parents2.
A creative mathematics teacher can lead a group of enthusiastic boys and girls on an adventurous mathematical journey and illustrate some elementary ideas relating to variables, equations, trial-and error method, number sense, mapping, problem solving, problem posing, graphs, mathematics in real life, connecting mathematics to other subjects in the school curriculum, etc.
Often, the curious and deep implications arising from folk mathematics are camouflaged by the popular and rustic context in which it finds itself. I am reminded of the essay ‘A mathematician’s apology’ by G H Hardy in which he reflects on chess and mathematics. He says, ”A chess problem is genuine mathematics, but it is in some way ‘trivial’ mathematics. However ingenious and intricate, however original and surprising the moves, there is something essential lacking.”
In conclusion, folk mathematics is a wonderful opportunity for a classroom teacher to get children interested in several aspects of mathematics but this requires some special efforts before implementation. It can fortify mathematics teaching and a teacher can use it in the classroom for homework, in assemblies, cultural programs, math mela and so on to offer an enriching and learning experience to the students.
References
1. Diophantine problems have fewer equations than unknown variables and involve finding integers that work correctly for all equations.
2. Incidentally, the solution is this: There are 5 men, 1 woman and 94 children.
The author has taught in Rishi Valley School in the past and is an independent consultant and teacher trainer now. He lives in Mysore and can be reached at sngananath@gmail.com.
